Database Storage

Disk-Based Architecture(磁盘架构)

DBMS 假定数据库的主存储位置在非易失性磁盘 (Disk / SSD);
系统组件负责在 volatile memory(主存) 与 non-volatile storage(磁盘) 之间移动数据;

Storage Hierarchy(存储层次)

CPU Registers < CPU Cache < DRAM < SSD < HDD < Network Storage

越靠上速度越快, 容量越小, 成本越高;
DBMS 设计目标: 最大化利用高速层, 最小化慢速访问;

为什么不直接用 OS 管理存储

虽然可以用 mmap() 将文件映射到内存, 但:

  • DBMS 无法控制 page replacement 策略;
  • OS 不保证 flush 顺序;
  • 并发写入下可能引发不可控的 page fault;
  • 因此 DBMS 自己实现 Buffer Pool, Page Replacement 与 Flush 策略更可控;

常见 OS 辅助机制:

  • madvise: 告诉 OS 访问模式;
  • mlock: 锁定内存页;
  • msync: 强制同步内存与磁盘;

File Storage(文件存储层)

数据库通常由一个或多个文件组成(专有格式);
OS 不理解文件内部结构;
Storage Manager 负责:

  • 管理数据库文件;
  • 控制页的读取, 写入与空间利用;

Page(页)与 Page Directory(页目录)

DBMS 将文件划分为固定大小的 pages(如 8KB);
Page 是 DBMS 的最小读写单位;
每页有 Page ID(逻辑编号), 通过 Page Directory 映射到磁盘偏移;

类型 大小 含义
Hardware Page 4KB 设备级写保护块
OS Page 4KB 操作系统级内存页
Database Page 512B–16KB DBMS 管理单元

Page Layout(页布局)

Page Header
记录页元数据, 如 Page size, checksum, 事务可见性等;

Tuple Storage
朴素顺序追加易产生碎片;

Slotted Page(槽式页结构)

Slot Array 保存每个 tuple 的偏移位置, 支持变长记录与高效删除更新;

Storage Model(存储模型)

模型 设计思想 应用场景
Row Store (NSM) 一行完整存储 OLTP, 频繁小更新
Column Store (DSM) 按列分块存储 OLAP, 聚合扫描快

Hash Tables

DBMS 在执行层需要高效的数据结构来支持索引查找, join, 聚合等操作;
核心结构包括:

  • Hash Table
  • Tree (B+Tree)

设计关键点

Hash Function

  • 将任意 key 映射到有限桶用 int 表示;
  • 常见实现: CRC-64, MurmurHash, CityHash, XXHash, FarmHash;
  • 目标: 快速且冲突率低;

Hashing Scheme
解决冲突的策略: Linear Probing, Chaining, Extendible Hashing, Linear Hashing;

Static Hashing(静态哈希)

哈希桶数固定, 冲突需处理, 插入过多会触发 rehash;
优点是简单, 缺点是扩展性差;

Linear Probing(线性探测)

删除策略:

  • Tombstone 标记删除;
  • Movement 移动填补空洞; 也就是将删除位置后面的元素前移;

对于重复的 key 就是直接插在现在的后面位置上

Chained Hashing(链式哈希)

对于可能重复的 key 可以对每个 hash 结果维护一个 linked list;
collision 冲突时元素挂到链表尾部;
插入, 删除, 查找都需遍历链表;

典型实现: Java HashMap;

Extendible Hashing(动态哈希)

对于 chain hashing 的方案, 当链表过长时, 触发 bucket split; 由于映射范围是 int, 因此可以等价于一个二进制树, 也就是通过 bit 长度来表示 chain 的容量;
因此如果要增加 chain 的数量, 就需要增加 bit 长度; 但是问题在于, 现在要做的是拆分现有的 long-chain, 比如 0x110 的 chain 过长, 那么最直接的方法就是扩张 bit 长度, 比如从 3 位扩张到 4 位, 也就是这个 chain 可以拆分成 0x1100 和 0x1101 两个 chain;

Extendible Linear Hashing

每个 hash entry 都有一个指向下一个同 entry (hashed key) 的 block 的指针, 也就是链表, 如果要扩展, 思路就是把超载的 node 重新分裂为 hash_2(key) = hash(key) % 2n;
类似于 extendible hashing, 但是不是通过 bit 长度来扩张, 而是通过一个全局的 depth 来控制; 直接

Tree Indexes

Index 的定义

Index 用于快速定位 tuple; 但是 index 也是存在 trade-off 的, 即更加精准的 index 可能会带来更高的存储与维护开销;

DBMS 需保证表与索引一致;
多个索引需平衡存储与维护开销;

B+Tree 结构

B+Tree 是平衡树的一种变体, 确保:

  • 数据有序
  • 支持 O(log n) 复杂度的查找, 排序和删除
  • M-way (一个节点有 M 个子节点) 平衡树;
  • perfectly balanced (每个 leaf 都在树中的深度相同)
  • 每个节点 (非 root) 都是至少 half-full (在这个节点内部的 key 数量: M2−1≤#keys≤M−1\frac{M}{2}-1 \le \# keys \le M-1)
  • 每个 inner node 如果有 k 个 key 就至少有 k+1 个非空子节点

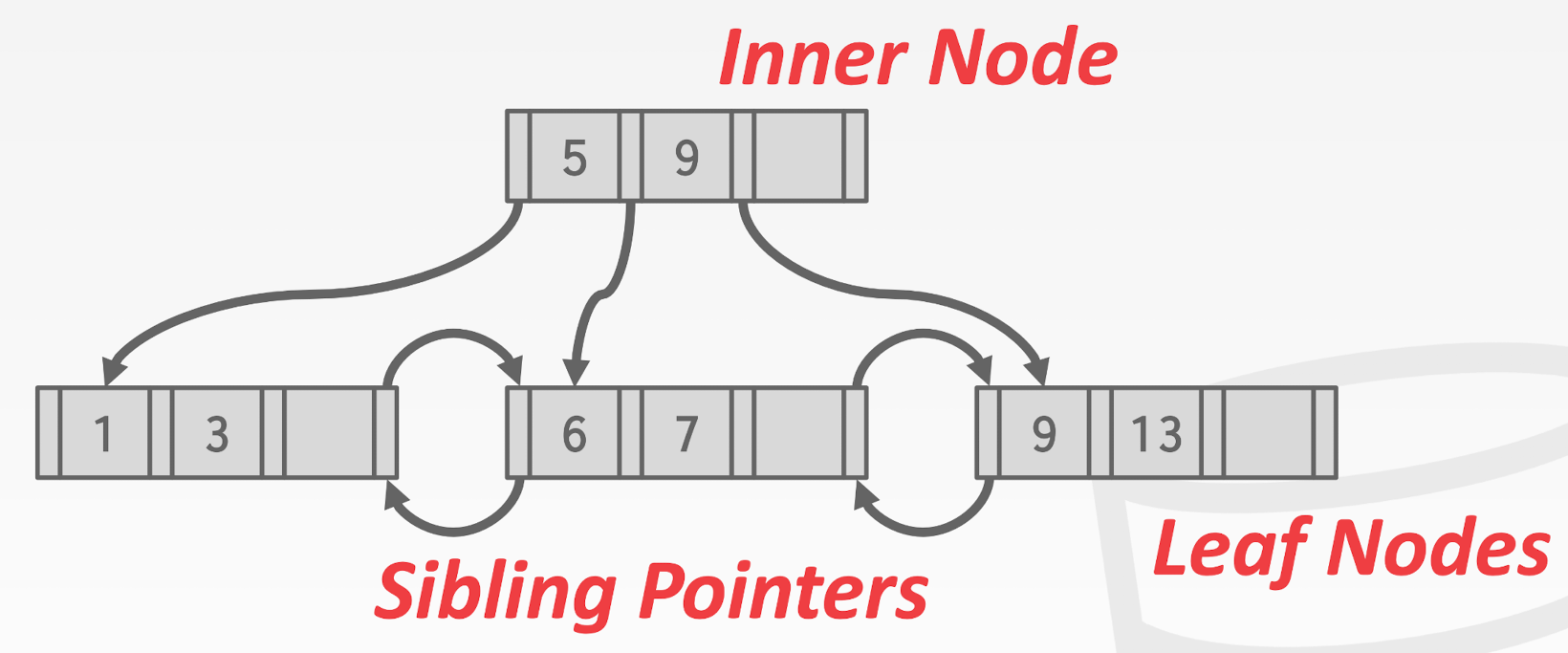
b+Tree_concept.png

从这个图的特点我们可以看出来, B+Tree 其实是有两种查找/遍历的方式的: 如果想要直接遍历所有, 就直接走 sibling ptr 从头到脚, 但是如果有 range 的话就可以走 tree 节点将查找复杂度直接开 log

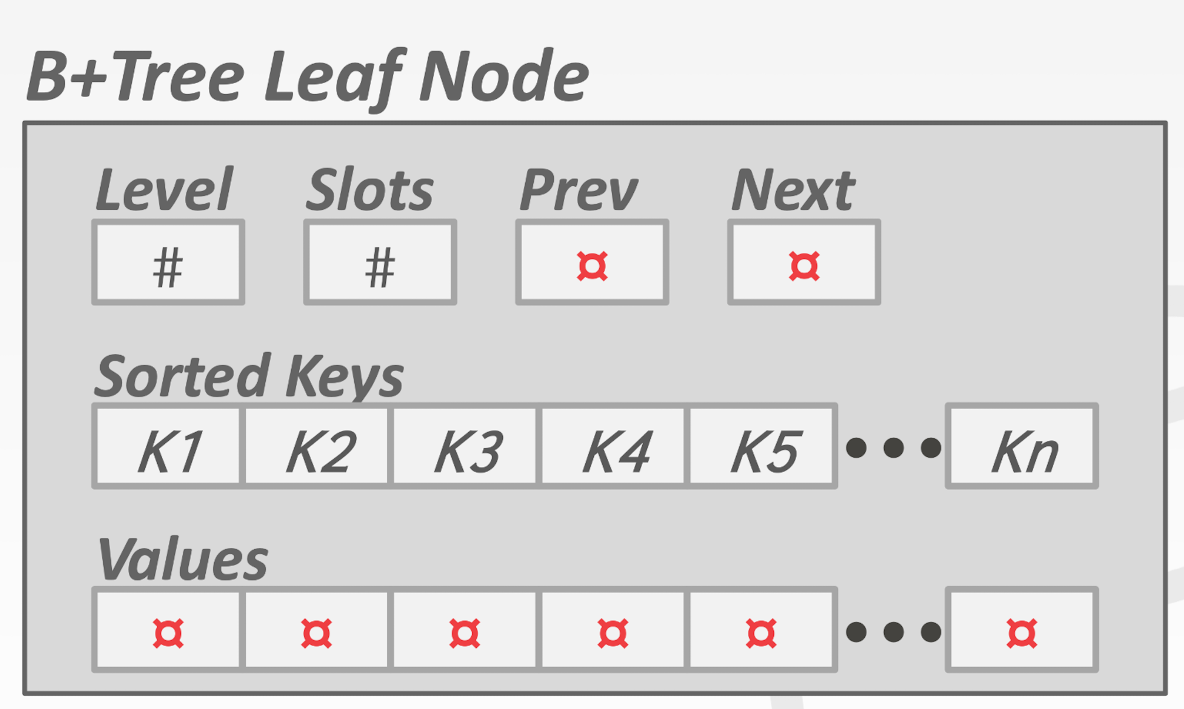
如图所示, 这里的每个 tree node 的数据结构都是如下:

1
2
3
4
struct b_plus_tree_t {
 Node_t* node, // points to the child node/sibling node
 T key 
}

这里确保: node 指向的 node 的所有数据都小于 value
如果是 leaf node, 那么这里的 node 一般是 PageID, 也就是 sibling 节点的地址

用 DB/FS 的角度来考虑, 这里每个 B+Tree node 就是一个 key/value pair array, 占据一个或者多个 page. 这里的 array 一般都是有序的 (基于 key)

b_plus_tree_leaf_node_concept.png

查找, 插入, 删除复杂度 O(log n);

这里的节点存储内容有不同的实现选择, 比如可以存储指向实际存储位置的指针, 也可以存储完整的数据结构 tuple

  • 存储 Tuple 的我们称为 Early Materialization
  • 存储 Record ID 的我们称为 Late Materialization

Insert

  1. 找到目标叶节点;
  2. 插入并排序;
  3. 若 overflow 则拆分;
  4. middle key 上推父节点;

Delete

  1. 找到目标叶节点
  2. 删除;
  3. 若低于半满则借 key 或合并;
  4. 合并需更新父节点;

Duplicate Keys

有两种解决办法:

  • Append Record ID: <key, rid>;
    • 这样每个 实际 key 就真的是 unique 的了
  • Overflow Leaf Node: 溢出节点链表;
    • 这个比较难以实现

Clustered B+Tree

这就是上面提及的, 在 tree 中存储的不是 索引指针, 而是直接存储整个 tuple 原始数据

Sorting & Aggregations

External Merge Sort(外部归并排序)

Phase 1: Sorting

  • 读入可容纳 page;
  • 内存内部排序;
  • 写回磁盘为有序 runs;

Phase 2: Merging

  • 多路合并;
  • 生成更大 run;
  • 直到全局有序;

2-way external merge sort

首先从最直接而二元外部归并排序开始做

  • Pass 0: 将每个 page 从内存中读取出来分别做内部的排序
    • 时间复杂度就是 O(n), 处理量是 #page * 2 因为有出有进
  • Pass 1/2/…: 递归地开始执行归并排序, 使用 3 个 buffer page
    • 2 个 buffer page 分别用来存储两个需要合并的 page
    • 1 个 page 用来存放输出

这个操作的复杂度是 (对于 N 个 page):

  • pass 数量: 1 = log2(N)
  • I/O cost: 2N * (# pass)

Join 算法

一个 query 的执行可以形成一个 tree 结构, 数据从 leaf node 经过各种操作符 (operator) 最终到达 root node 输出结果
而整个 root node 输出的内容就是此次 query 输出的结果

  • Early Materialization: 在 join 过程中就将 tuple 的完整数据都读入内存
    • 优点是后续不会再需要回到 base table 来读取数据
  • Late Materialization: 只在 join 过程中读入 tuple 的 record ID (其实就是 join key), 最后再根据 record ID 读入完整数据
    • 更加适合 column 存储, 因为这样只需要读取非常少的列数据

最基本方案的 Cost 分析

假设现在有两个表 R 和 S, 分别有 M 和 N 个 page, 以及 m 和 n 个 tuple (是指表中总的 tuple 数而不是单个 page 内的 tuple 数量), 那么遍历式的 Nested Loop Join 的 cost 就是: M + (m * N);

为了让这个 Cost 更小, 要将 m 和 N 尽可能地变小, 也就是减少外层循环的 tuple 数量和内层循环的 page 数量

如果要使用 block 来进行操作, 也就是每次读取都是按照 block (整个 R) 为单位进行读取, 那么 cost 就是 M + (M * N), 也就是要小的 block 在外, 大的 block 在内

但是显示情况下往往能够使用的 buffer 的尺寸是有限的