Overview

本简报回顾了分布式系统中逻辑时钟的核心概念, 其在处理事件排序方面的必要性, 以及它如何解决传统时间戳的局限性;重点介绍了"先行发生" (Happens-Before) 关系, Lamport 逻辑时钟的构造与规则, 以及如何通过扩展逻辑时钟实现分布式系统中的全序 (Total Ordering);

分布式系统的时序共识背景

分布式系统被定义为"a set of distinct process, 通过 exchange message 进行通信, 具有 non-neglegible communication latency, 并 not sharing fate";
这意味着系统中的不同部分:

  • 在空间上是分离的
  • 它们之间的通信存在延迟
  • 并且一个部分的故障不会自动导致其他部分的故障

关键问题

  • 状态依赖性: 如果对消息的响应取决于该消息以及(某些)过去的消息, 那么计算就是有状态的 (stateful);这通常建模为有限状态机;
  • 容错性与复制 (Fault-Tolerance and Replication): 为了容忍故障 (这里主要指网络或者机器坏了), 需要对状态进行复制; 复制副本之间必须相互通信, 由于通信延迟不能忽视且未知, 因此复制副本在时间上是分离的
    • 意思是当完成复制的时候时间戳应该是创建主机上的, 表示在创建的主机上完成了第i个操作之后进行缓存
    • 但是这个时钟和存贮主机的时钟如果没有共识或者说不一致, 那么这个时间戳就没有意义了;
  • 保证一致性: 必须保证复制副本的"答案"最终一致; 这通过"保证单一的更新顺序"来实现;
    • 如果两个机器上进行的操作并发但是顺序不同, 导致结果有细微差异那么在这两个主机的备份内容就会不一致

传统时间戳的局限性与因果关系

在分布式系统中, 不能使用"挂钟"时间(wall-clock time)来强制执行事件排序, 因为:

  • 时钟漂移: 物理时钟会漂移, 导致__不同机器上的时间不一致__;
  • 单调性可能被违反: 时钟同步是具有挑战性的, 因为"timestamp is X"的消息可能被任意延迟; 即使假设对称延迟 (RTT/2= transmition delay), 也并非总是如此, 有时我们需要更强的保证;
  • 核心思想: “A little ‘not knowing’ makes some things easier.”

因果 (Causal) 关系

逻辑时钟基于因果关系的概念, 即事件 A 是否可能影响事件 B;

  • 这里的 可能 的意思是 A 的输出传递给 B, B 视为一个函数, 可以对传入做任意处理, 所以是可能影响
  • “如果 A 可能影响了 B, 那么 A 必须在 B ‘之前发生’;”
  • “如果 B 可能影响了 A, 那么 B 必须在 A ‘之前发生’;”
  • “如果两者都不是真的: 事件排序’无关紧要’;”

逻辑时钟: 保证因果顺序

逻辑时钟"保证保留因果关系(重要的事情), 允许任意排序不重要的事情;" 这其实是一种削弱的排序, 只要求保持部分有序, 那么其实就是拓扑排序的思路

术语定义

  1. A “happens-before” B (A -> B): “当且仅当 A 可能是事件 B 的输入的一部分”;
  2. C “is-concurrent-with” D (C || D): “当且仅当 C 不 -> D, 且 D 不 -> C”;

目标: 我们希望有一组"时间戳" T, 使得"如果 A -> B, 那么 T(A) < T(B) 得到保证";
注意: 反之不一定成立 “T© < T(D) 不意味着 C -> D”;

定义先行发生关系的三种事件

分布式系统中有三种事件:

1. 内部事件 (internal events)
2. 发送消息 (send events)
3. 接收消息 (receive events)

先行发生关系的规则

  1. 同一进程内: “在同一进程中, 如果 a 发生在 b 之前, 那么 a -> b;”
  2. 消息传递: “如果 c 是消息 b 的接收事件, 那么 b -> c;”
  3. 传递性 (Chain Rule): “如果 a -> b 且 b -> c, 那么 a -> c;”

Lamport 逻辑时钟的构造

Lamport 逻辑时钟(也称逻辑时钟)通过以下规则将先行发生关系编码为时间戳:

初始化: "每个进程 PiP_i 维护一个本地时钟 CiC_i", 初始值可以任意;

时钟更新规则

  1. “在执行事件之前, CiC_i -> Ci+1C_i + 1;” (每个事件发生前, 本地时钟递增)
  2. “如果事件 B 有一个内部前驱 A, 那么 T(B) 必须大于 T(A);”
  3. 消息发送规则: “在任何消息 M 中发送本地时钟;”
  4. 消息接收规则: "在接收时, 将时钟 CjC_j 设置为 1+max⁡(Ci,C(m))1 + \max(C_i, C(m))", 其中 C(m)C(m) 是消息中携带的发送方时钟值;
  5. “如果事件 R 是某个消息 M 的 接收 事件, 并且 M 是作为事件 S 发送 的, 那么 T® 必须大于 T(S);”

时钟条件

  1. “每个事件 e 都有一个时钟时间 C(e);”
  2. “如果 a -> b, 我们保证 C(a) < C(b);”(通过构造证明)
  3. “反之不成立: C(j) < C(k) 不保证 j -> k;”

应用于复制状态机(RSMs)

复制状态机要求"机器必须按 LC顺序 应用所有操作", 即"必须有一个所有事件的单一全局顺序";

核心思想

“每个操作 O 都有一些逻辑时钟时间 T;”
“当我知道所有其他复制副本至少已推进到 T(O) 时, 才应用 O;”
这意味着"我们已经收到了所有 U -> O 的更新;"
如何知道这一点? “收到一条发送时间 S >= T(O) 的消息;”

处理并发事件

“如果两个事件 A 和 B 之间: A 不可能是 B 的(直接/间接)输入, B 也不可能是 A 的(直接/间接)输入;”
“那么我们可以以任何顺序应用它们;它将产生一个可能发生的顺序, 没有人能说它不是实时发生的顺序;”
六, 生成全序(Total Ordering)
Lamport 逻辑时钟虽然保证了因果顺序, 但无法保证所有并发事件在所有副本上都具有相同的相对顺序;为了实现全序, 可以扩展逻辑时钟:

Break Tie: “通过将节点 ID 附加到每个事件来打破平局;”
全序规则: 进程 Pi 用"时间" Ci(e).i 标记事件 e;
C(a).i < C(b).j 当:
“C(a) < C(b) 或者”
“C(a) == C(b) 且 i < j”
"没有两个事件会有 C(a)==C(b) 且 i==j;"因此, “所有事件都被(全局地! )排序;”

Communication & Acknowledgement

在分布式系统中, 知道对方收到了消息(例如"foo() 已修复, 可以预期")是一个挑战;

相互告知: "你必须告诉我! ","我必须告诉你! "这种"我知道你收到, 你知道我收到, 我知道你知道我收到…"的递归问题似乎无解, 无法最终验证是否具有确认收到的信号;

解决方案: “heartbeat 心跳消息” 是一种方式;
"任何消息交换都会更新时钟, 即使是那些只为了更新时钟的消息! "(例如, “still alive!”)

LC 的特性和局限

  • 事件而非时间 (Events, not time)
    • Lamport "时钟"并不测量物理时间, 而是事件的因果链长度
  • 独立漂移 (Independent drift)
    • 不通信的节点逻辑时钟可以随意漂移, 但不影响一致性
  • 因果与影响 (Causality & influence)
    • 因果性表达观察者对结果的期望
    • 并发事件虽然无因果, 但需在所有副本保持相同顺序

LC 两个共识性应用

因为 LC 确保的事件的因果顺序 (Causal Relationship), 但是如果两个在 LC 定义下是并发的事件, 那么它们顺序是可以任意的, 但是在实际的分布式复制情况下, 这种并发并不一定好:

比如 中国银行有两个数据中心分别在北京和上海, 北京的数据中心有一个操作是利息10元, 上海有一个操作是扣税 1%, 那么二者实际上并不存在逻辑的因果关系, 但是其先后顺序会影响到一个用户的最终存款项内容 (这里的数学问题更加像涨薪10%和减薪10%)

分布式设计者的目标是确定一个 total order (不一定对用户最有利, 尤其是雇佣方是银行).

但是 LC 在逻辑上已经给了一个因果全局时钟共识, 我们这里要做的应该是利用这个共识来实现 (非因果) 操作上的逻辑一致

参考计算机界有名的 (图灵) 状态机设计, 如果一个状态机的输入是确定的, 那么其输出也是确定的 deterministic

利用 Lamport Clock 的因果顺序, 我们可以在 分布式系统中实现两种关键的共识机制:

  • RSM (Replicated State Machine) 复制状态机
  • Primary/Backup 主备复制

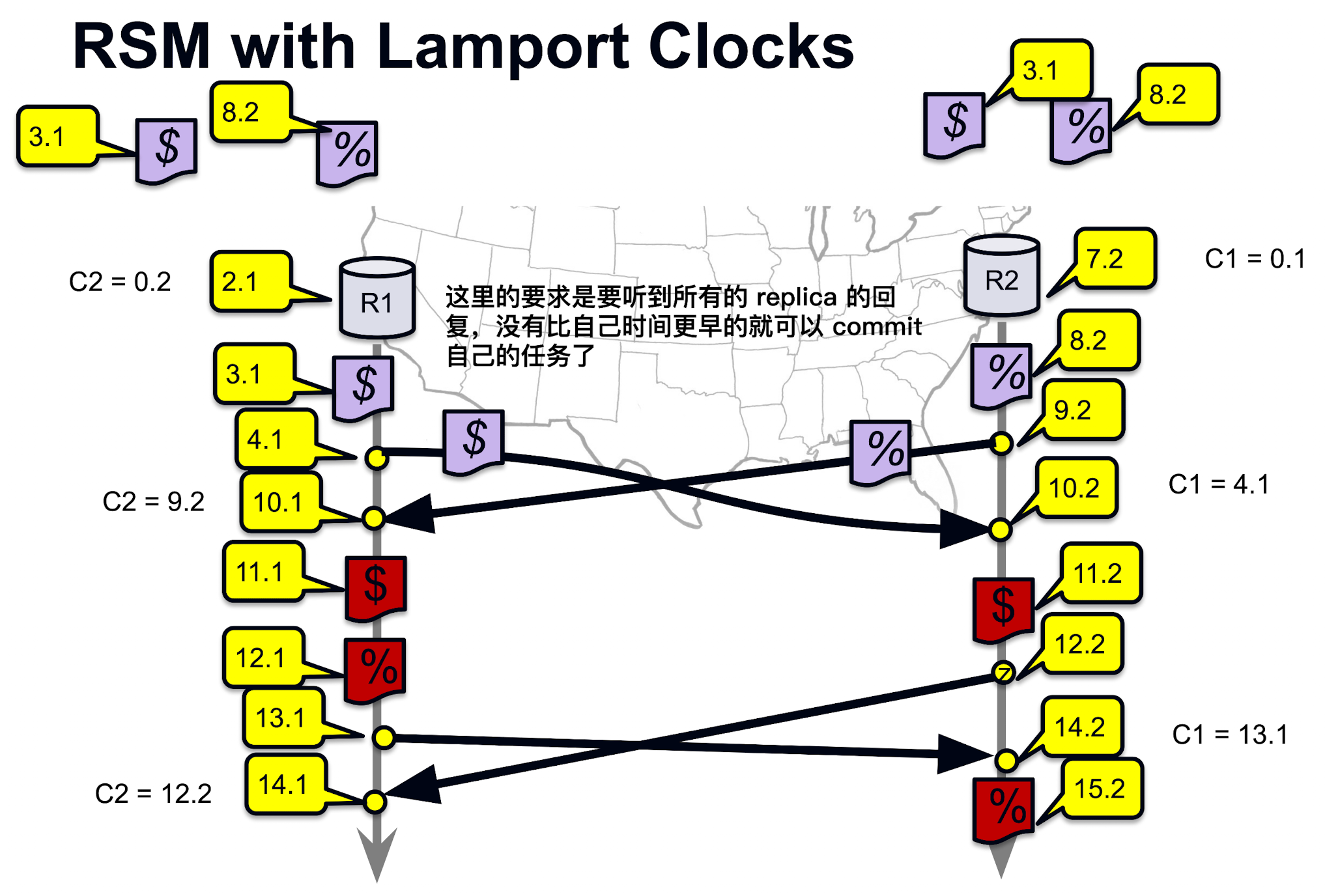
复制状态机 (RSM, Replicated State Machine with Lamport Clocks)

状态机复制是实现容错服务的一种常规方法, 主要通过复制服务器, 并协调客户端和这些服务器镜像间的交互来达到目标
– Wikipedia

  • 算法原则
    • 每个操作 (operation) 都带时间戳 (timestamp, 但是这里指的是 Lamport 时钟的时间节点)
    • 仅当所有副本都至少推进到该时间戳时才能执行
    • 队列 (queue) 按时钟顺序存储待提交更新
    • 可以确认无更早更新时提交队首元素
  • 等待问题 (Waiting)
    • 可能需要等待很久(若没收到其他副本消息)
      • 包括网络延迟和网络断联, 节点宕机等
      • 比如上面的例子中, 北京的数据库更新的一个新的存款, 而上海如果没有收到北京的更新, 就永远无法提交这个更新(上海根本不知道发生了什么)
    • 心跳 (heartbeat) 交换时钟, 证明存活
      • 前面简单提及过, 如果用 Ack 来验证收到, 可能会陷入无限递归
    • 可用 undo log 容忍临时不一致 (temporary inconsistency)

/images/rsm_consistency.png

RSM 方案局限与问题

  • 失败阻塞 (Failure blocking)
    • 如果某个副本宕机, 其他副本可能被阻塞无法提交, 因为节点依赖于其他所有在线的 node 成功 commit 的反馈
    • Lamport 时钟在失败场景下成为"死胡同" (因为 LC 完全依赖于 communication 来实现局部 consensus 从而递推达到全局 consensus)

主备复制

解决 RSM 的一个方法是使用 主备复制 (Primary/Backup Replication);
这会在下一份笔记中详细介绍

对比总结 (Comparison Summary)

特性 (Feature) 复制状态机 (Replicated State Machine, RSM) 主备复制 (Primary/Backup Replication)
一致性 (Consistency) 所有副本按相同顺序执行操作 (deterministic order) 主节点先执行并同步到备份 (primary first, then backup)
排序机制 (Ordering) 借助逻辑时钟 (Lamport clock) 或向量时钟 (vector clock) 主节点天然决定顺序 (primary decides order)
容错能力 (Fault tolerance) 副本失败可能导致阻塞, 需要共识协议支持 (e.g. Paxos, Raft) 主节点失败需选举新主, 备份失败相对容易替换
性能 (Performance) 通常需要额外消息交换, 等待所有副本确认 性能较高: 客户端只与主交互
一致性模型 (Consistency model) 可实现强一致性 (linearizability), 但依赖协议复杂度 保证外部一致性 (external consistency), 内部可暂时不一致
适用场景 (Use cases) 分布式数据库, 强一致性存储系统 任务分配器 (MapReduce Master), 银行账户等主从式系统