1. 密码学基础

Message Integrity 信息完整性

定义

ensures that attackers cannot modify a message w/o being detected.

MITM 模型

传输部分

• 并不完全相信网络的信息的真实性
• 希望 Bob 接收到的完全就是 Alice 发出的信息
  

威胁模型 threat model

• Mallory 可以 see/modify/forge(伪造) message
• Mallory 的目的是让 Bob 相信一个不是由 Alice 发出的信息

防御威胁的方法论

verifier 验证器

如图所示，在发送的时候额外传送一个验证码，即要求验证码 $v = f(m)$

random function 完全随机函数

• 被 A/B 容易计算，但是不容易被 M 计算 (即不被知道)
• 如果被找到 $x\neq m$ 且 $f(m) = f(x)$ 的 collision 就失败了
• 表示方法：用一个很大的表格记录映射关系，需要内存非常大
• 优点: 完全安全，即 M 除了瞎猜没有更好的方法
• 缺点: 不切实际，如上其需要非常大的存储内存

pseudorandom functions (PRF) 伪随机函数

由 $2^n$ 个函数群组成，即 $f_1()\cdots f_{2^n-1}()$ 其中下标是 A/B 才知道的

• efficiently computable
• no efficient function that can distinguish btw a PRF or a random oracle (因为完全随机函数不现实，这里用 oracle 来形容)
  因此有了如下的定义，通过 5 步流程定义安全的 prf:
  
  也就是说经过多次的尝试 M 仍然不能以显著高于 0.5 的概率猜出面前的机器是伪随机还是完全随机那么就认为是安全的

pseudorandom generator (PRG) 随机生成函数

程序中随机获得一个随机数是怎么做的？往往用一个 uniform random 函数来选
这个过程往往是继承于物理过程 (Heisenburg), 而在 Turing Machine 的抽象中并不存在
函数定义：

$g_k: \bot\to \{0,1\}^n$

其中 k 为一个完全随机数，称为 seed 种子; n 为关于 k 长度的多项式 poly(|k|), 其安全性的定义类似于 PRF

操作系统随机数

一般程序的随机数由操作系统进行提供，其中 seed 大多数来自于物理世界和 os 的交互，例如时间、外部硬件输入等

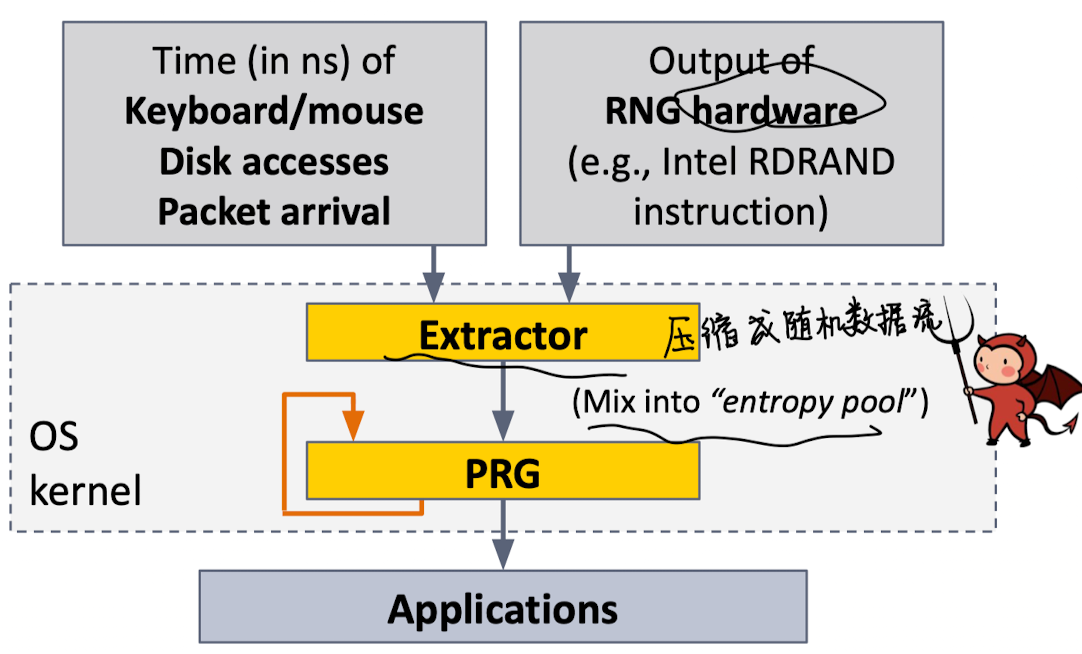
通过 extractor 提取器将数据提取出来并且标准化，然后通过 prg 进行生成，从而产生难以被攻击者预测的随机数；
即使一个攻击者获取了熵池的状态，但这个过程是transient(短暂的)可以通过系统再次注入新的随机性恢复安全，但是这个过程的快慢是操作系统方向正在处理的问题

Kerckhoff’s Principle

由19世纪荷兰密码学家提出，即密码系统的安全性应该依赖于密码的秘密性而不是系统的安全性设计

密码学哈希函数

输入是一个随机长度的内容，输出是一个固定长度的内容
满足以下三个要求:

• preimage resistance
  • 对于给定的 h 很难找到输入 m
• collision resistance
  • 很难找到两个m使得 $H(m_1) = H(m_2)$
• second-preimage resistance
  • 对于给定的 $m_1$ 很难找到 $m_2$ 使得 $H(m_1) = H(m_2)$

SHA-256 加密方法

需要构建一个压缩函数，将输出分裂成一定长度并且输出为一定长度

Merkle-Damgard (MD) Construction

1. 将输入内容填充为 512bit 的整数倍长度
2. 如果本身是 512 倍数那么久再填充 512 bit
3. 对每个 256bit 长度的块进行加密映射
   

Length_Extension Attack

这是针对 md 加密函数的一种攻击方式，可用于 sha256 等
对于初始加密操作 $y = H(x)$, 且密文 x 未知，则攻击者可以延长输入的内容为

$z = H(x || padding || s)$

其中 padding 根据 md 构建方法一般是填充 $\text{0x80(0x00)}^*$ 即对于给定长度其 padding 填充内容是固定已知的; s 是攻击者自己加入的密文
注意对于原文也应该增加 padding 部分, 即 z 不是由 $x||s$ 直接连接映射得到的
而且上图公式中的 padding 并不存在于最初的 y 的求解过程中，这个 padding 是哈希函数在处理 x 的时候自动补充的，即对于 z 的获得其最后的新 padding 由新字符串获得

反 lea 算法: HMAC

MAC 指的是 Message Authentication Code, 是一种特殊的 verifier, 输入为随机长度的 key, 输出为固定长度

HMAC construction

将一个任意哈希函数 $H()$ 变成一个 MAC

$HMAC_k(m) = H(k\oplus c_1 || H(k\oplus c_2 || m))$

其中 $c_1$, $c_2$ 是两个公有的常数, $\oplus$ 表示的是 xor 异或操作
类似于双层哈希函数映射

• inner hash: $H(k\oplus c_2 || m)$ 表示密文 m 可以和 k 通过一定程度的处理之后进行加密
• outer hash: $H(k\oplus c_1 || inner)$ 得到一个外部映射，除非知道密钥 k 否则无法解密或者攻击
  由于在传统 hash 函数中，会存在 $H(m)||H(s) == H(m||padding||s)$ 但是在 HMAC 函数中，2 层哈希映射不会导致这类问题

数据的机密性 Confidentiality

定义

在信道上发送加密之后的数据，eavesdrop 无法知道原文是什么
模型如下:

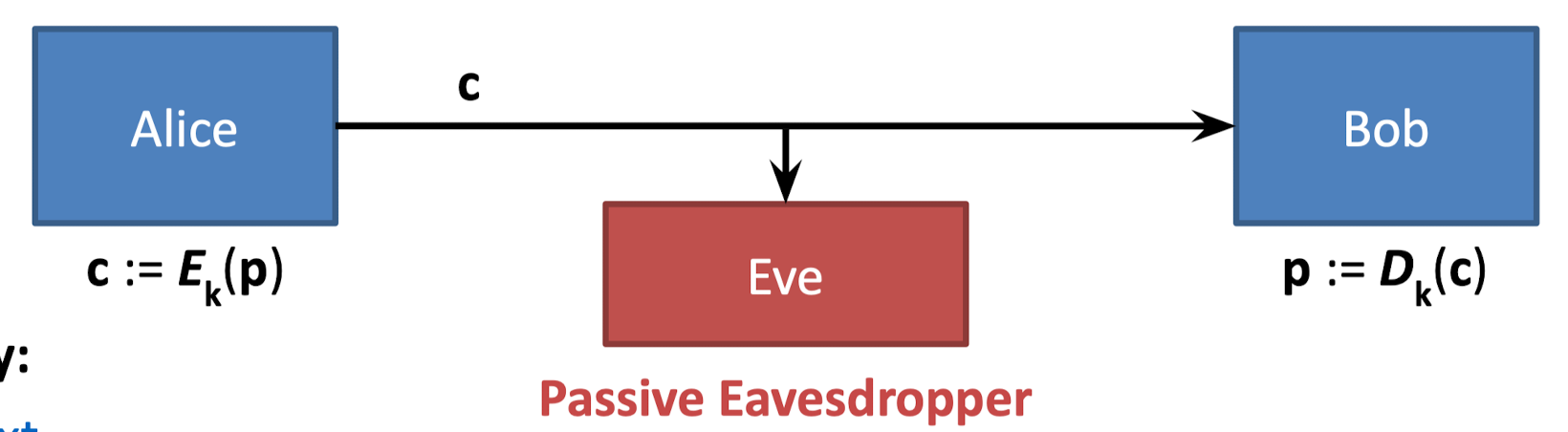
机密性的侧重点和完整性不同，机密性需要将密文在知道密钥的情况下高效解密，而完整性只要求证明没有被修改过

凯撒密码 Caesar Cipher

将每个原文通过沿着字母表顺序加减进行变换得到的密文
破解的方法是查看频率最高的字母是哪个，一般是 e > t > remainings

Vigenere Cipher

将凯撒密码的思路变成每 n 个字母为一个关键词，关键词内逐个增大字母表顺序

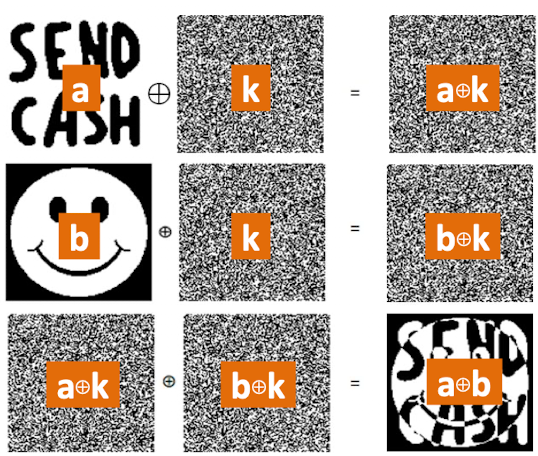
One Time Pad (OTP)

当 Alice 和 Bob 共享一个较长的随机bit密钥的时候，可以实现完全安全的加密，但是由于双方很难同时拥有大量的共有密钥，因此不是很现实
且不能两次使用同样的 pad，因为对于同一个密钥 k 原文 a, b 通过加密得到 $a\oplus k$ 和 $b\oplus k$ 但是通过 $(a\oplus k)\oplus (b\oplus k) = (a\oplus b)$ 可以将原数据部分泄漏出来

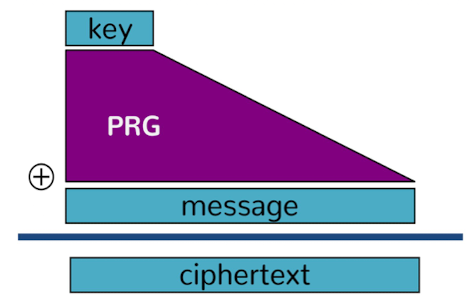
Stream Cipher: 流加密

通过 PRG 构建机密性, 即收发端采用同样的密钥k用于prg函数 $g_k$ 来进行生成以及解码
不可以重复使用密钥，不可以重复使用 prg output bits

最常用的 prg 函数 ChaCha20

Block Cipher 块状加密

块状加密算法使用的是固定尺寸的块与一个可以复用的密钥 k

$E_k(p) :\{0,1\}^{|k|} \times\{0,1\}^{n}\to \{0,1\}^n$

且有一个逆映射来解密这个密码块，使用同一个密钥

$D_k(c) = E^{-1}\_k(c): \{0,1\}^{|k|}\times \{0,1\}^n\to \{0,1\}^n$

这样对任意的k 都有 $D_k(E_k(p)) = p$
实际上 k 可以有 $2^n$ 种可能，这个加密函数解和 prf 的区别是这里要求可以且方便做逆映射

伪随机排列 PRP

一个安全的 prp 是一个函数无法从完全随机排列和随机函数区分开来的，最常见的算法是 AES

AES 块状加密

以 128 bit 为块状尺寸，可用密钥长度 128，192，256b
对应地一般执行 10，12，14 个 rounds
会从 k 上产生对应 round 数量的 subkey 从而对数据进行多轮的使用伪随机密钥的加密

padding: PKCS7 算法

通过对结尾 padding 填充数量进行对应的内容填充可以得到相应结果，即五个空填充 05 05 05 05 05

ECB 电子代码簿模式

对多个密码块进行加密，如果是对各个密码块各自地进行加密，由于使用同一个加密算法，相同内容的明文会被加密成相同内容的密文，因此，可能会被频率分析给攻破

CBC 代码块链状模式

为了解决上述 ecb 的同类加密问题，采用链式加密方法进行加密，即每一块的密文给下一块的解密文进行 xor 处理进行二次解密/加密防止
最初情况下需要选定一个完全随机的 initialization vector IV

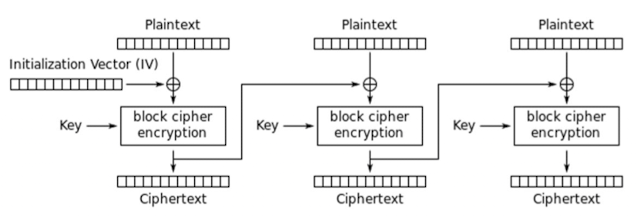
但是这个算法不能并发或者错序解码，因为解码需要依赖前一个 block 的内容

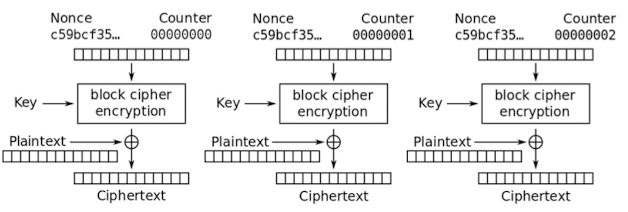
Counter (CTR) mode

将分组密码转换成流密码，通过生成一个密钥流 $s$ 和 $k$ 以及一些随机唯一的 nonce

$s:= E_k(nonce||0)||E_k(nonce||1)||\cdots$

也就是通过一个计数器生成一个密钥流 s 然后与原明文进行 xor 加密，这样可以避免模式泄漏，也能支持并行处理，效率较高, 但是 nonce 不能重复使用 (在一次流加密内是相同的，但是两次之间的 nonce 是不同的，即保证 s 的不同从而避开 block cipher 的普遍问题)

失效的边界情况

• 长度保持加密: 需要保证加密前后的数据长度保持不变 (cbc会发生填充, ctr会额外传输nonce)
• hard disk encryption
• format-preserving encryption: 对于 格式有一定要求的密码需要使用其格式进行加密, 使用 padding 和 nonce 会打乱这种阵型

Padding Oracle Attack

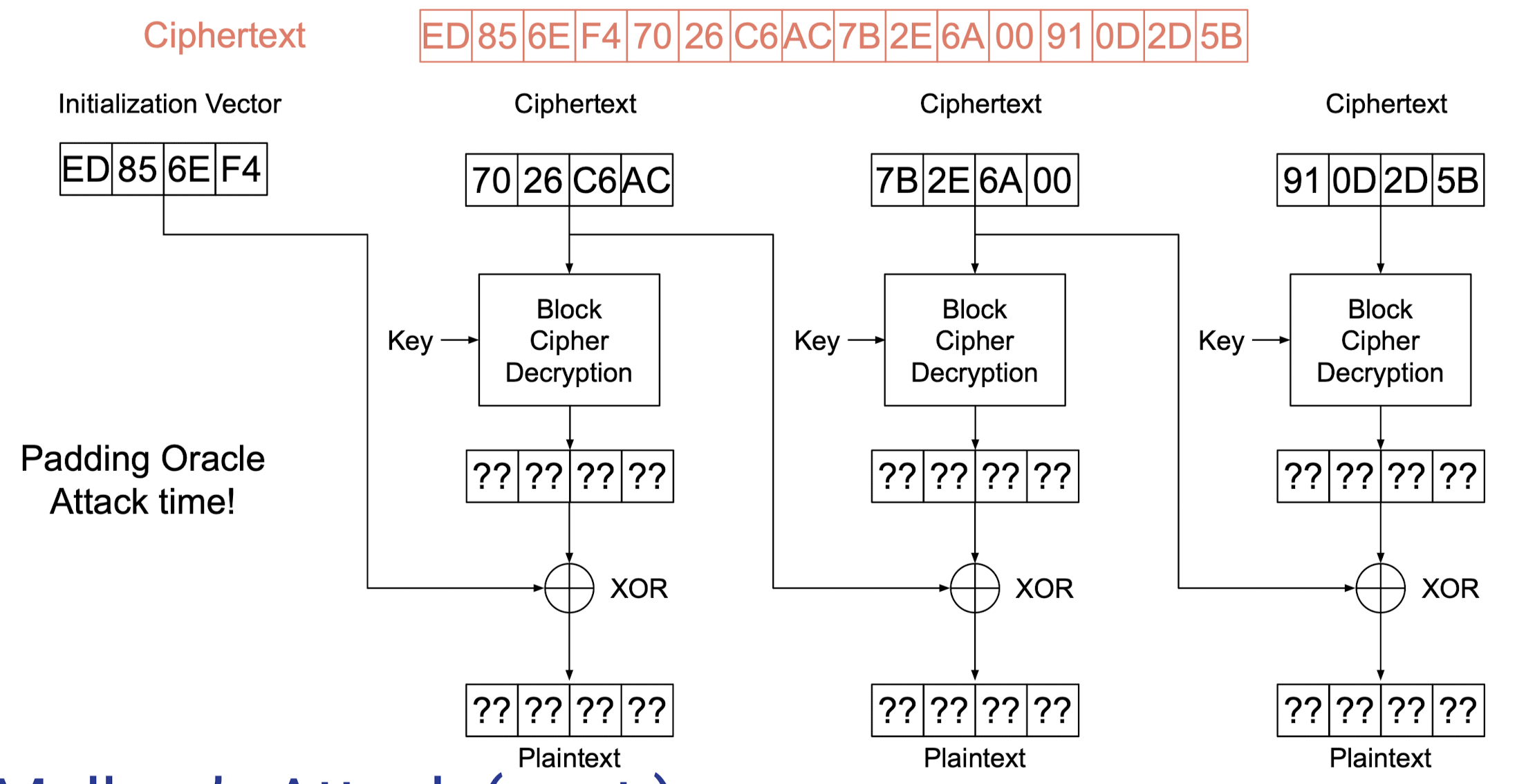
在设计解密算法的时候，输入值 ciphertext 已知，输出值 plaintext 已知，即对于 $C_k\oplus D_{k+1} = P_{k+1}$ 知道 $C_k$ 和 $P_{k+1}$, 且对于第 k+1 步的解密过程，$C_k$ 只起到 xor 的功能，因此其不应该能影响到 $D_{k+1}$ 的满足 padding 职能，故在标准的 D 下通过更改 C 的最后一位可以形成唯一合理的 P 这一过程 D 保持黑箱，但是一旦找到合法的 $C_k, P_{k+1}$ 对，则可以求解 D 的值，再带回原 C 就可以获得标准的 P 解.
攻击者利用了这个特性和等效公式 $C_k \oplus P_{k+1} = D_{k+1}$ 逆向求解 D, 即利用padding的长度，因为无论最后的padding是多长，可以假设长为 1，然后不断试验 $C_k$ 的最后一位来找到对应的值 (即直接通过多次改 $C_k$ 并且执行解密算法后检查最后一位是否为 0x01),

机密与完整性的结合

Malleable 可塑性

指一个密文可以被修改为另一个密文，且解密之后含义发生有效更改，操作者不一定知道原来密文的内容

Authenticated Encryption 认证加密

有两种常用方法：

• 简单将mac认证和加密合起来
• 发明一个具有两种功能的算法
  公式描述

  $c:= E_k(p)$

  $p/\text{fail} := D_k(c)$

  解密函数可能会返回 fail 如果检测到密文 c 并不是经过其加密算法获得的结果，例如在 padding oracle attack 的时候服务器经常会返回 invalid_padding 等状态就是 D() 检测到了问题

安全性形式判断

注意 $D_k^*()$ 表示的是修改之后的解密函数，如果输入的是前一问加密成功的结果，会被故意修改为 fail 输出，其余遵循标准的解密流程，这样攻击者无法通过重放旧密文来进行攻击，消除 oracle 的优势

Composing 加密法

即上述将 mac 认证和 加密结合起来的算法，有三种顺序: MtE, EaM, EtM

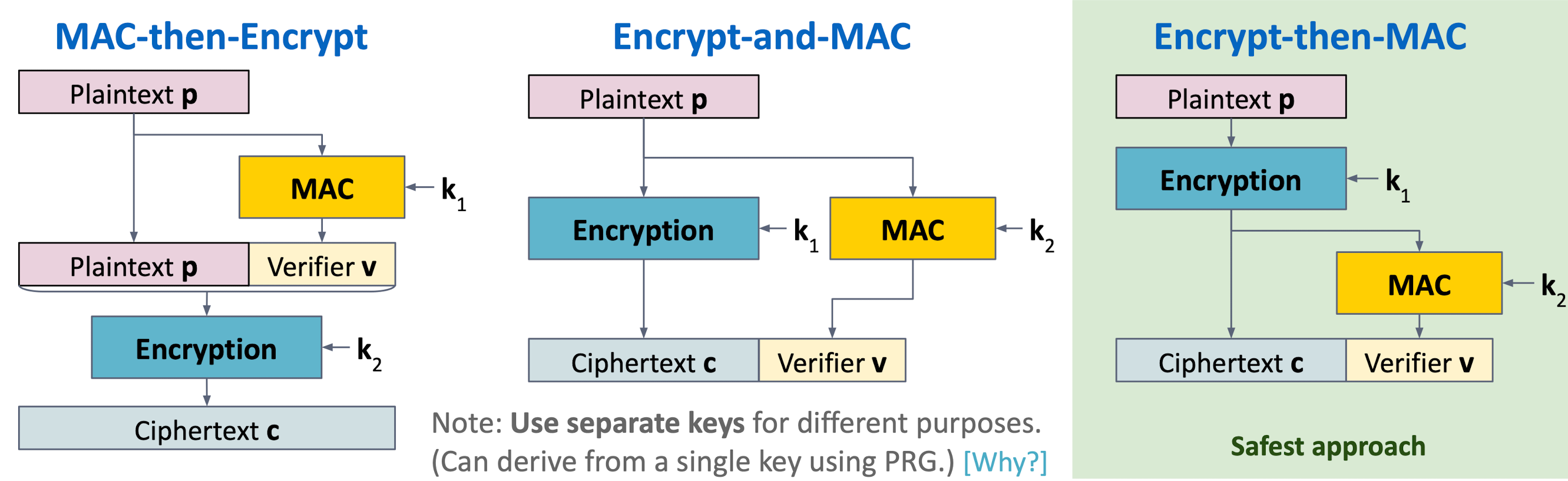
但是三者中只有 EtM 是最安全的，因为它的 MAC 是基于密文产生的
EaM 的 mac 是基于 明文产生的，攻击者可以只修改密文的前面一部分而不被发现，例如对 http 只修改 message body 而不修改 header, 而 mac 可能只验证header部分，从而导致基于 header 明文计算得到的 MAC 仍然通过
MtE 有可能会在解密阶段被破解，
EtM 下修改任意密文都会导致 MAC 失效 (因为 MAC 基于加密密文产生，二者一一对应)

关联数据认证加密 AEAD

这是一种常见的 all-in-one 二合一加密算法

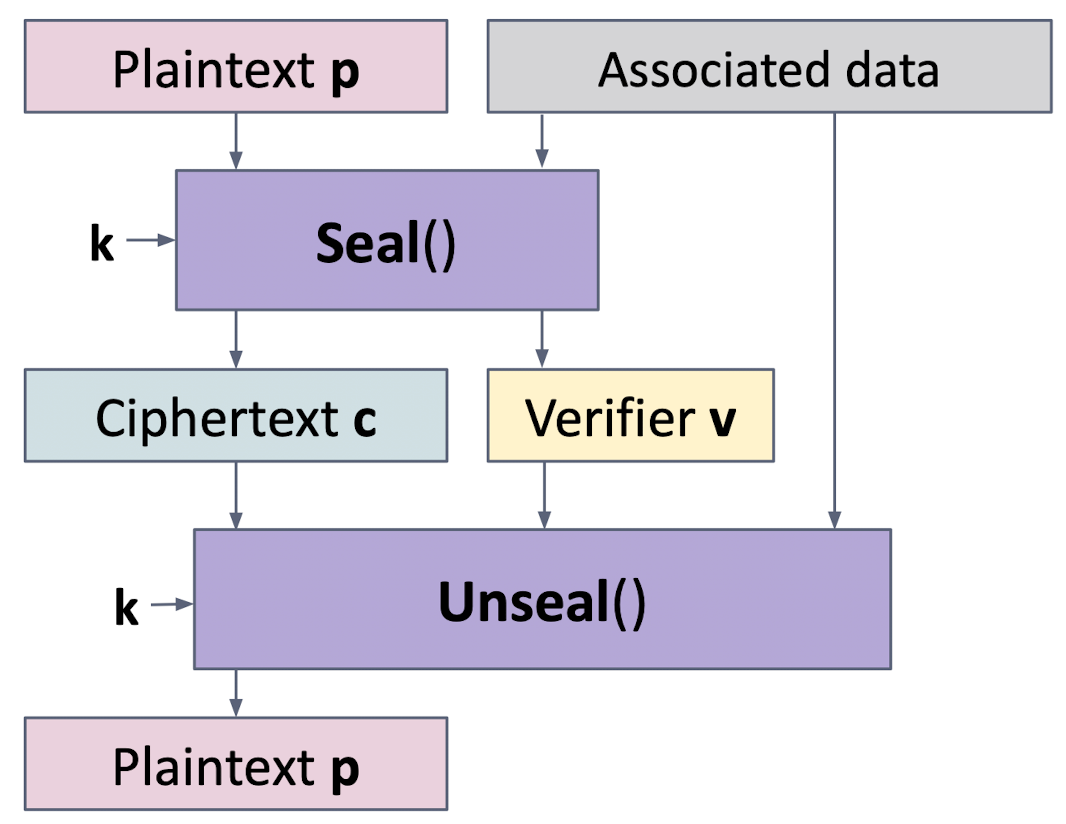
图中的 v 为验证标签，由明文加密得到，加密过程中会用到 associated data 但是其本身并不会发生加密，通过明文进行传输，完整性用 v 进行保障
该算法可以将关联的数据参与到加密过程中来，例如用计数器/http的body数据 参与加密等
其中密文公式:

$c,v = Seal(k,p,[ad])$

解密公式:

$p, err = Unseal (k,c,v, [ad])$

如果错误返回的是 err 信息
常见的算法有 AES-GCM, ChaCha20-Poly1305

密钥交换与公钥加密

DH 密钥交换

在公有的信道上可以看到 1. modulus $p$, 2. primitive root $g$ 3. 密文 $g^a \mod p$, $g^b \mod p$

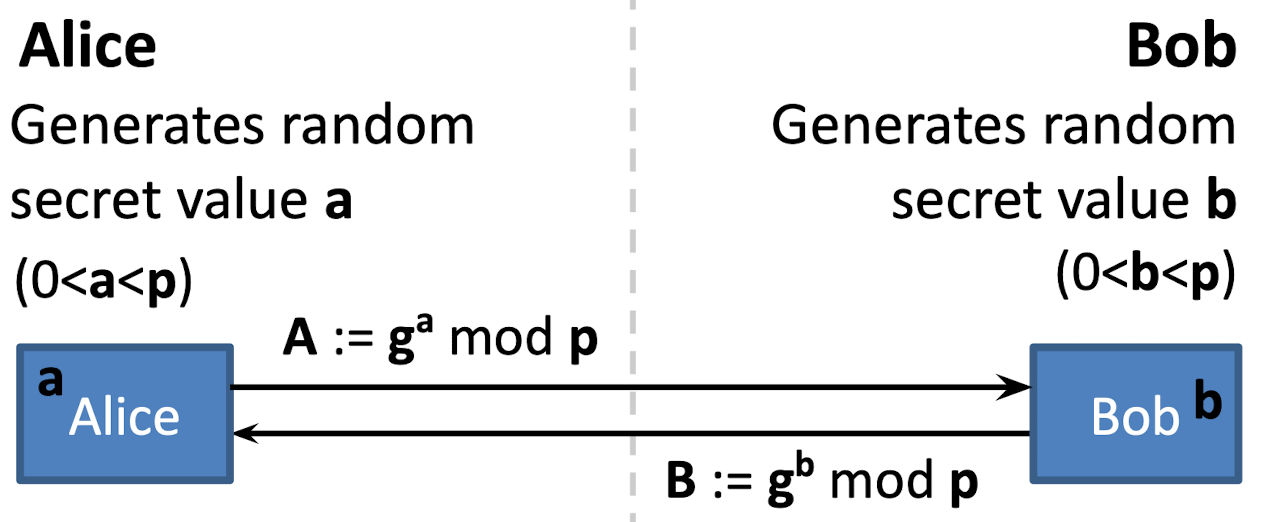
公钥内容是 $g^{ab}\mod p$

优点

可以防御被动窃听问题 (确保机密性)，即 eve 窃听模型

缺点

无法防御 MITM 攻击模型，即无法保证信息的完整性，可以在接受公钥的时候利用 g 和 p 设定自己的专门密钥 $a'$ 来计算自己的专门密钥 $g^{a'}\mod p$
这样别人收到的信息就被攻击过了

解决方案

1. trust-on-first-use: 假设第一次交流并没有收到攻击，那么使用第一次的密钥就行 (SSH)
2. comm out-of-band:
3. digital signatures: 数字签名, 其中 https 常用

前向安全 forward security

即使长期密钥被泄漏，也可以保证前面的通信数据不会被解密
DH 密码交换可以保证每次对话都使用各自的新密钥，防止某一次的密钥破解引起大量秘密泄漏

RSA 公钥加密

学院派 rsa (Textbook RSA)

公钥 $(e, N)$ 密钥 $(d,N)$

公钥加密

c = m^e\mod N$$, $$m = c^d\mod N

公钥认证

签名：

$s =m^d\mod N$

验证：

$m = s^e\mod N$