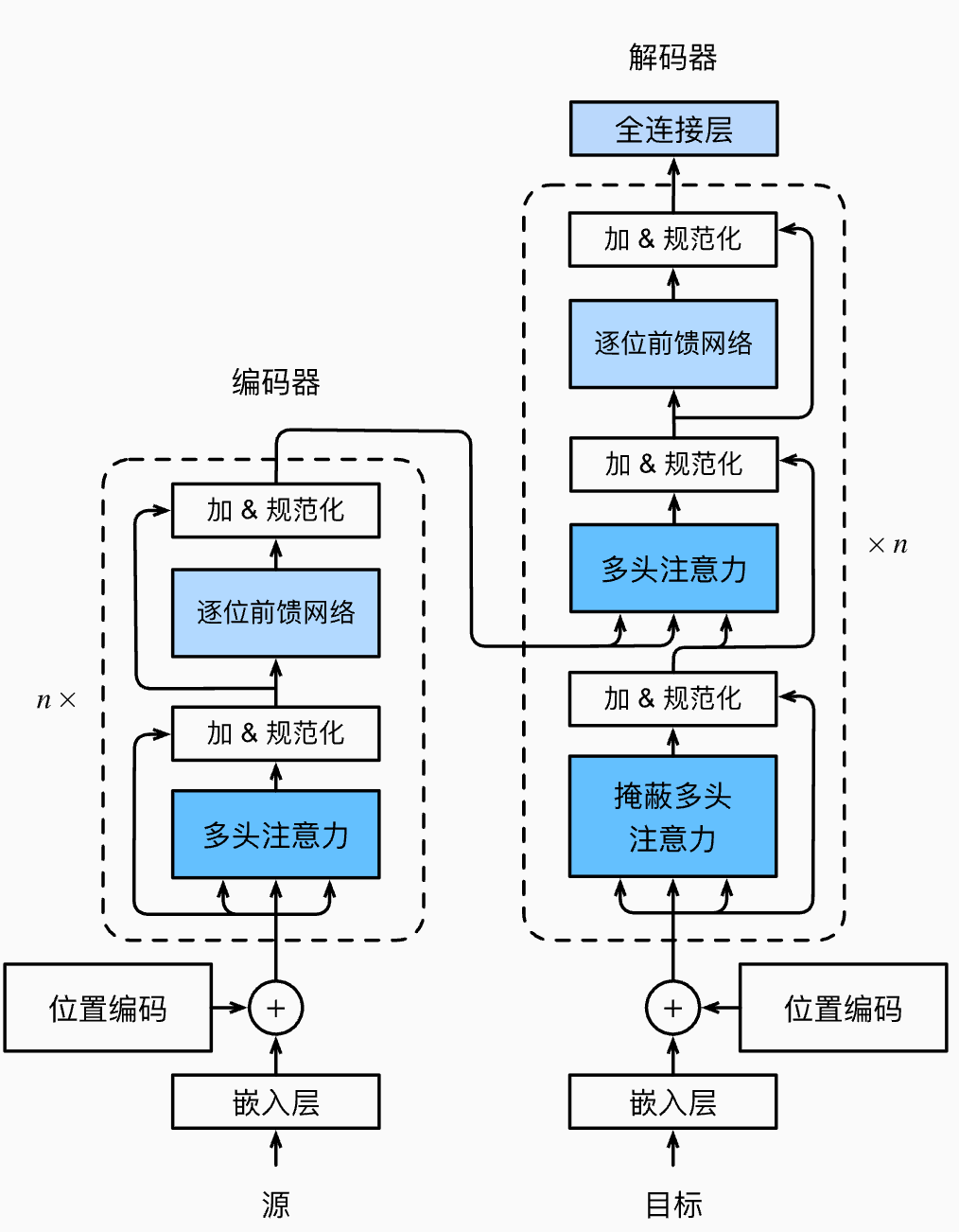
注意力机制到 transformer

背景 —— 从生物学说起

注意力会收到主观提示的引导，在深度学习中，也要设计一种能及时将注意力转移到某个感兴趣的角度的机制

查询 query, 键 key 和 值 value

定义自主性提示为查询, 也就是在输入一个 key (非意志线索) 的时候，通过输入一个查询将全连接层转变为一个注意力汇聚层，并且将汇聚之后的内容称为 值, 从而实现注意力的有向汇集与输出。

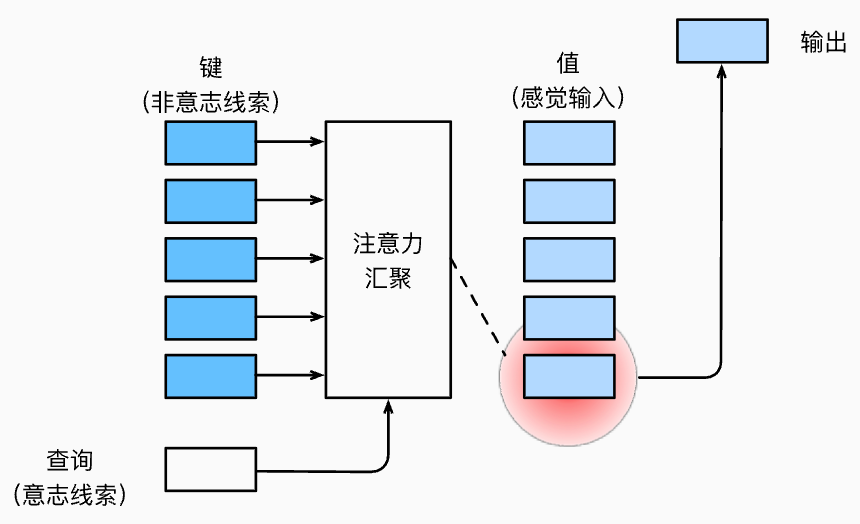
概述: 注意力机制通过注意力汇聚将查询（自主性提示）和键（非自主性提示）结合在一起，实现对值（感官输入）的选择倾向，这就是与 CNN 等模型的关键区别。

注意力汇聚：Nadaraya-Watson 核回归

背景问题

假设要拟合预测一个非线性函数

$y_i = 2\sin x_i + x_i ^ {0.8} + \epsilon, \epsilon\sim N(0,.5)$

其中 $\epsilon$ 是一个噪声项，利用 numpy 生成 50 个 truth 数据集

平均汇聚

定义最简单的平均值计算为平均汇聚 estimator

$f(x) = \frac 1 n \sum_{i = 1}^n y_i$

那么由于结果不收敛，其估计效果会很差
因为这个估计方法忽略了输入 $x_i$, 也就是我们说的注意力是平均散开的而没有汇聚

NW 汇聚

NW 算法是一种非参数注意力汇聚方法:

$f(x) = \sum_{i=1}^n \frac{\kappa(x - x_i)}{\sum_{j = 1}^n\kappa (x - x_j)} y_i$

注意看，这个函数中使用的是 x 与 $x_i$ 的关系来确定对 $y_i$ 的占比大小，从理解上应该是二者越接近则 越使用 $y_i$ 的数值
上述函数对输入的位置进行了加权平均，其中 $\kappa$ 函数表示了核函数 kernel, 也就是将一个低维非线性函数映射到高维空间中成为一个线性函数的映射, 或者重写上述函数表述为

$f(x) = \sum_{i =1 }^n \alpha(x, x_i)y_i$

这个公式称为 注意力汇聚 attention pooling 公式
也就是将查询 x, 键值对 $(x_i,y_i)$ 放到了一个公式中, 并且将查询和键一起称为 注意力权重 $\alpha(x,x_i)$ 注意这里的查询和键是同一类对象，且当 i-th 键与查询越接近则其映射的注意力权重会越大

放到一般的模型训练中，测试集合 (映射前的) 就表示查询，训练数据 (映射前的) 就表示键，根据上面的结论，如果 true value 和训练结果越接近，则其分配的注意力权重就越高
上述内容具有一定的局限性，即其学习不带有可优化参数，因此其对于不够充足的数据不会收敛到很好的结果，应该通过加入一定量的学习参数来实现深度学习的效果
最简单的例子就是在上述的高斯核函数改成 $\exp(-\frac 12((x-x_i)\vec w)^2)$

注意力评分函数 Attention Scoring Function

加性注意力

当查询和键是不同长度的矢量的时候可以使用加性注意力为评分函数，公式

$a(q,k) = w_v^\top \tanh (W_q q+W_k k))$

其中可学习参数为三个 w，维度 $W_q \in \mathbb R^{h\times q}$, $W_k\in \mathbb R^{h\times k}$ 因此可以理解为将查询和键连接起来放到一个多层感知机里面，其中包含一个隐藏层，隐藏层的单元数是 h 并且使用 tanh 作为激活函数，偏置项为 0

缩放点积注意力

在查询和键的长度一致的时候，可以通过点积实现高计算效率，公式为

$a(q,k) = q^\top k/\sqrt{d}$

多头注意力机制

对于单元注意力机制可以学习某一个具体行为，而多个注意力头组合起来捕获序列各种范围的依赖关系从而形成一个整体学习

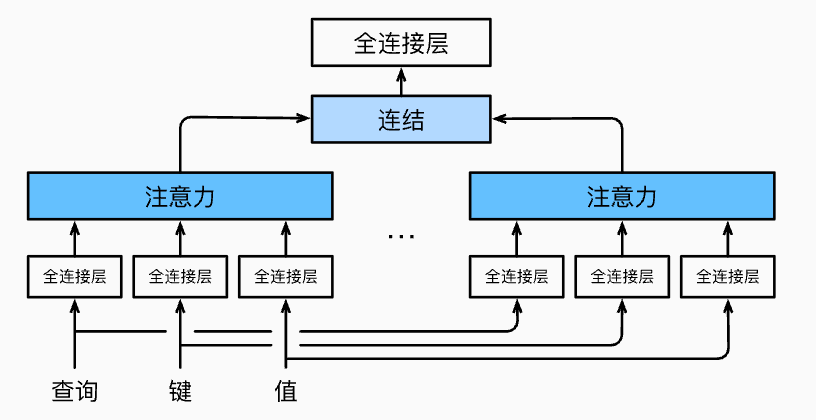
用公式将上述模型表述为:

$h_i = f(W^{(q)}_i q, W^{(k)}_i k, W^{(v)}_i v)\in \mathbb R^{p_v}$

其中 3 个 W 表示对应的权重矩阵，也是本模型可以学习的参数部分
而如上图所说，经过综合考虑多个单元注意力机制学习的行为，我们会得到多个输出的标量 (对应各个行为内容，且根据加性注意力评分函数的维度对齐写法，每个注意力输出的维度都是 h) 综合得到向量 $W_o = \begin{bmatrix}h_1\\\vdots\\h_h\end{bmatrix}$
如果要放到总的输出中还要对其进行 transpose

自注意力和位置编码

在 NLP 领域中，当输入一句话 (词元) 进行注意力汇聚的时候，往往会将同一组词元同时充当查询，键和值，即每个查询都会关注所有的键值对并生成一个注意力输出，这种方式称为自注意力 self attention

远距离依赖关系

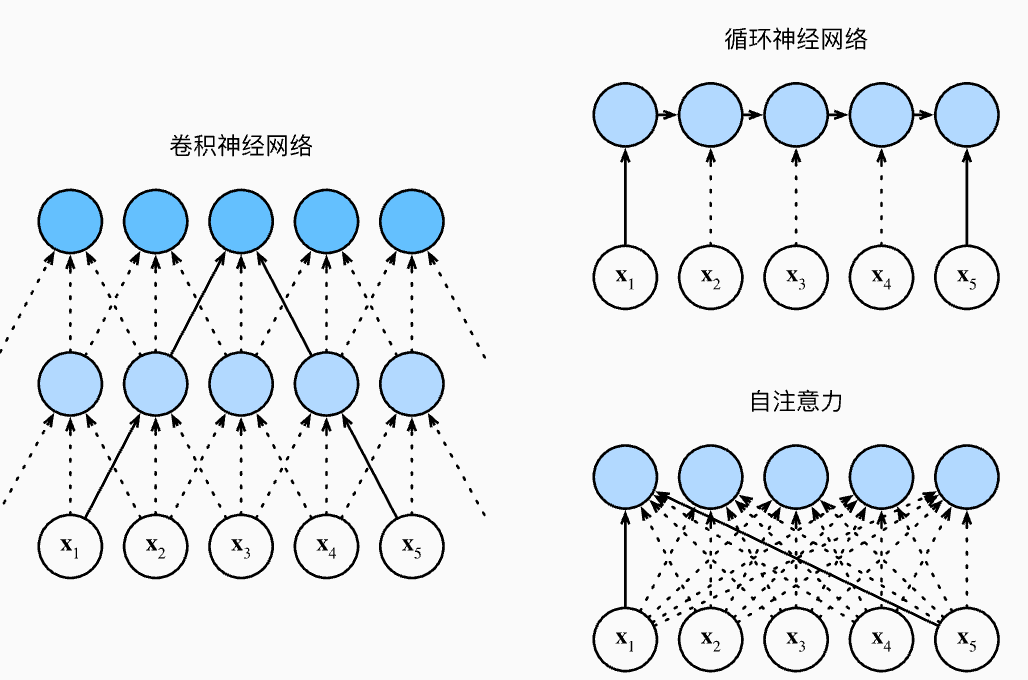
对比 cnn, rnn, self-attention 三种框架，其中 cnn 由于其 pooling 操作将特征汇聚到一起，从而只能注意局部的特征而对于远距离的依赖问题可能就很难处理好了；rnn 是序列结构，不能并行计算导致处理缓慢
self-attention 兼具并行快速处理和最大路径最短两个优点.

位置编码

相比于循环神经网络的逐个重复处理词元，自注意力使用了并行计算的快速操作而放弃了顺序操作，因此需要使用位置编码来注入绝对的或者相对的位置信息。
实践中往往使用 三角函数对位置进行编码，例如在位置编码矩阵中第 [i, 2j] 与 [i, 2j+1] 坐标的值应该为
$p_{i,2j} = \sin(\frac i {10000^{2j/d}})$ 和 $p_{i,2j+1} = \cos(\frac i {10000^{2j/d}})$
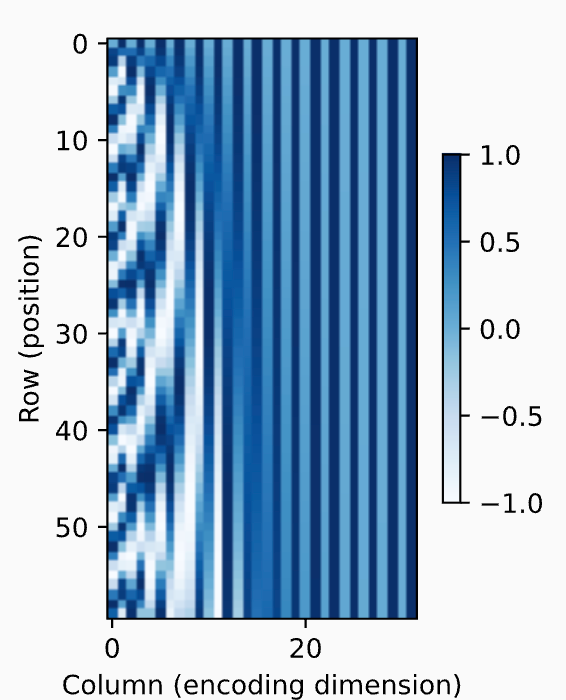
因此这个矩阵P从左向右频率会逐渐降低，周期逐渐变大，用二进制编码来理解，大概为 从低位到高位其周期频率逐渐降低的模拟，如下图为P矩阵值的热力图

Transformer 框架

由于