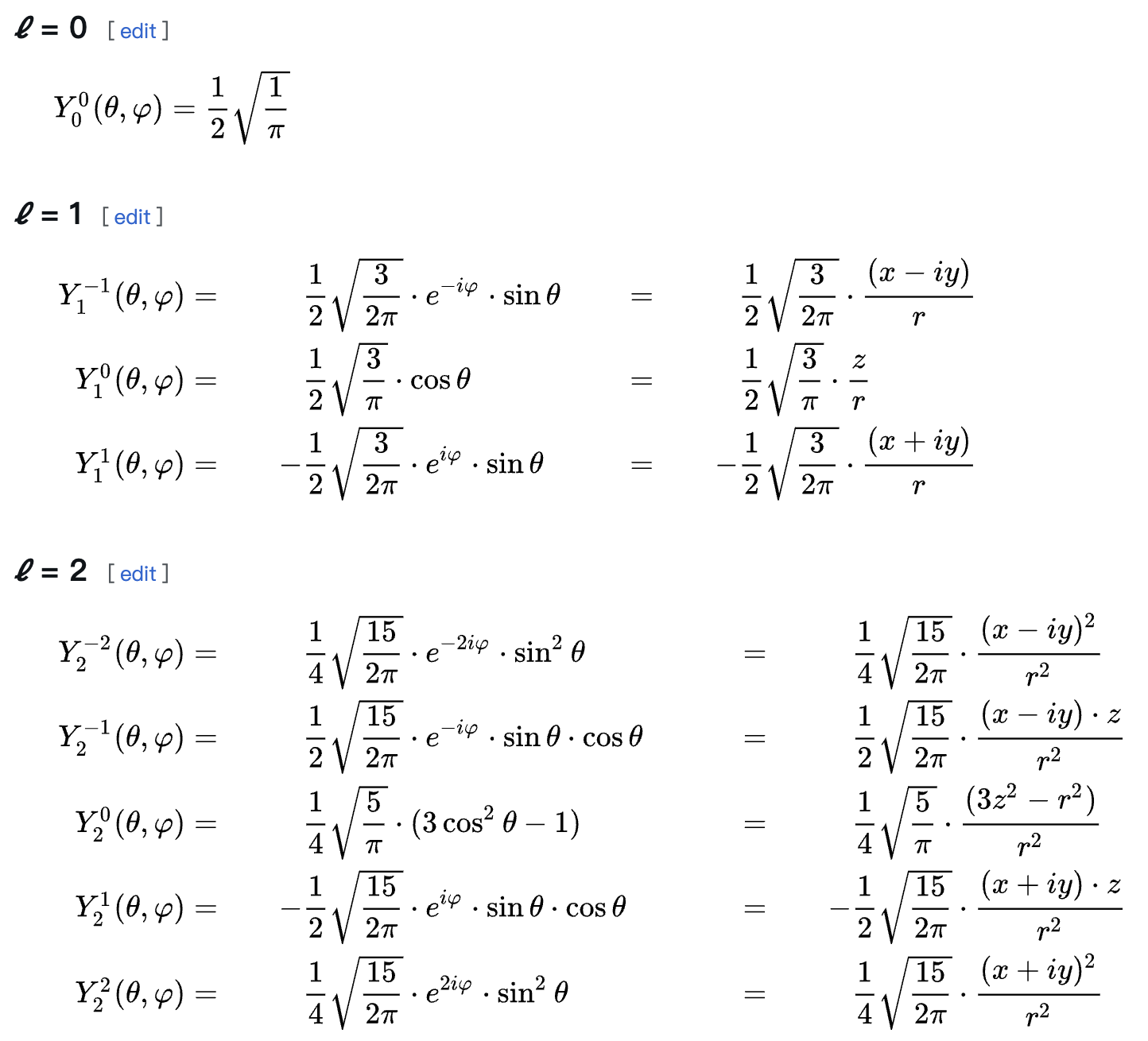2. Gaussian Splatting 高斯泼溅

Splatting 是一种点云的渲染技术，它的核心思想是将每个点云点以"斑块"或者"模糊点" (splat) 的形式投影到屏幕上，形成一个小的、带有一定宽度的圆形或椭圆形区域，以便填补点云中的空隙。这样可以使得稀疏的点云看起来更加连续和完整
在 Splatting 中，渲染器将每个点的三维位置根据相机视角投影到屏幕上的二维位置。为了让点的显示区域更大，渲染器为每个点分配一个近似圆形的小斑块区域，这个区域可以根据点的深度信息（与相机的距离）进行缩放。最终效果看起来是一个密集的、相互叠加的模糊点阵列

Splatting 泼溅过程

过程可以分成三步：选择雪球-> 抛掷雪球 -> 合成图像

高斯球

高斯椭球在此处定义为一个三维的概率分布模型，它通常有以下几个关键参数：

1. 中心位置（均值）：这个点表示我们“认为”物体的中心位置，或是物体最可能出现的位置。
2. 协方差矩阵：这个矩阵定义了椭球在不同方向上的延展程度，也就是位置不确定性的分布。协方差矩阵的值越大，表明在该方向上的不确定性越大。
3. 长短半轴：通过协方差矩阵可以计算出椭球的三个半轴长度和方向，它们对应了不确定性的三个主要方向。
   在高斯泼溅技术中，这个高斯椭球会被“泼溅”到图像或3D空间中，以表示物体在该区域内存在的概率。通过这样的模型，我们可以得到物体在空间中不同位置的概率分布，这对于物体识别和定位是非常有用的。

马氏距离 (Mahalanobis Distance)

为了在多维空间中定义类似一维的“距离”概念，我们引入了马氏距离，用于衡量点 x 到均值 $\mu$ 的距离，但它是通过协方差矩阵 $\Sigma$ 加权的

$D(x, \mu) = \sqrt{(x - \mu)^T \Sigma^{-1} (x - \mu)}$

简单理解马氏距离

考虑如下问题：

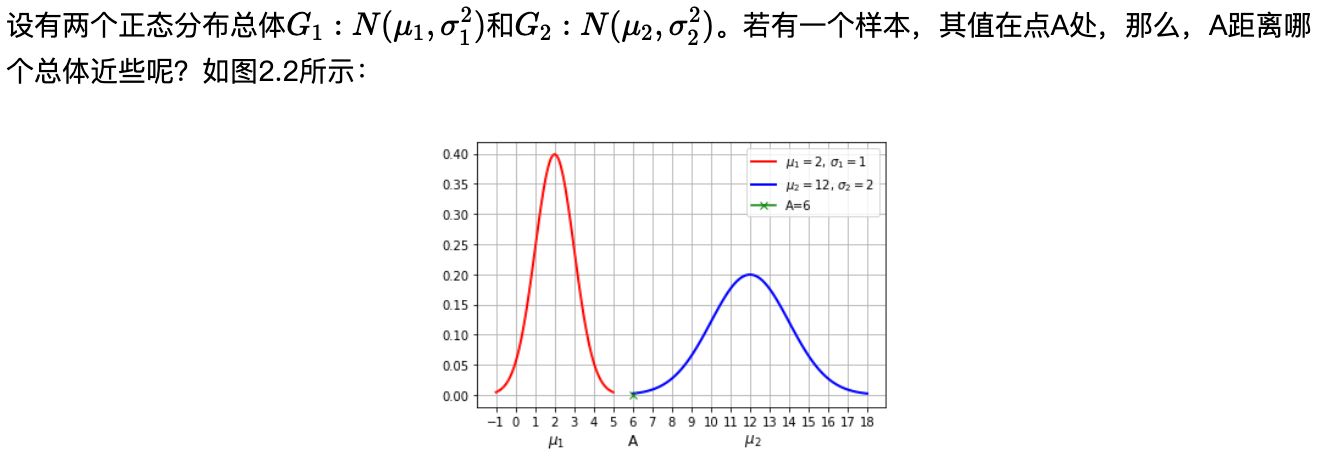
数据点 $A$ 到 $\mu_1$ 的距离是 2$\sigma_1$ 而到 $\mu_2$ 的距离是 3$\sigma_2$ 但是绝对距离又是到 $\mu_2$ 更近，因此需要将二者变成到同一个度量上进行讨论，我们称这个步骤为 标准化
对于一维正态分布随机变量直接使用 Z 值进行标准化，即 $\frac{x - \mu}{\sigma}$ 也就是会除以标准差, 那么对于一个高维变量, 我们可以使用 协方差矩阵来表示高维情况下的方差, 其中协方差矩阵 $M[i][j]$ 的值表示第 i 维度和第 j 维度变量的协方差
那么公式 $\vec v^T M \vec v = \sum_{i=1}^n\sum_{j=1}^n m_{ij} v_iv_j$ 可以理解为向量 v 不同维度的加权求和，或许可以简单理解为对向量 v 进行了平方操作, 在上述表达式中 $M = \Sigma^{-1}$ 表示的是协方差矩阵的逆，即可以理解为 $v^2 / \sigma^2$ 就是一维变量的扩展形式
综上所述，马氏距离表示的是高维样本 x 点到平均值 $\mu$ 的距离对不同量纲标准化的结果

高斯椭球的表达式

高维空间下的概率密度函数表示为:

$G(x) = \frac{1}{\sqrt{(2\pi)^k |\Sigma|}}\exp{(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))}$

或者直接用马氏距离进行表示

$G(x)=\frac{1}{\sqrt{(2\pi)^k |\Sigma|}}\exp{(-\frac 12 D(x,\mu))}$

注意这里的 k 是变量 x 的维度，简单理解为 多变量下就用对应数量个 $2\pi$ 并且用 $|\Sigma|$ 进行归一

为什么是椭球

以二维的情况为例，我们研究指数部分 $\frac{(x - \mu_1)^2}{\sigma_1^2} + \frac{(y - \mu_2)^2}{\sigma_2^2} -\frac{2\sigma_{12}(x - \mu_1)(y - \mu_2)}{\sigma_1\sigma_2} =$ const
那么这就是一个类似椭圆的表达式了，高维下同理
同时由于 G(x) 是一个区间 (0,1) 因为这是一个概率表达式, 所以其事实上是一个实心椭球体

从标准高斯分布到一般高斯分布

标准高斯分布的均值为 0, 标准差均为 1, 即协方差矩阵表述为 $\begin{bmatrix}1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$ 因此任意高斯分布的协方差矩阵可以表述为 $\Sigma = A \cdot I \cdot A^T$
因此对于一个标准随机变量的 仿射变换 $\vec w = A\vec x + b$, 我们有 $\vec w\sim N(A\mu+b, A\Sigma A^T)$ 而且可以将矩阵 $A$ 改写为旋转和伸缩的乘积 $A = RS$
最终我们可以得到论文中提及的等式：

$\Sigma = A\cdot I \cdot A^T = RSS^TR^T$

再对矩阵进行特征分解

$\Sigma = Q\Lambda Q^T = Q\Lambda^{0.5}\Lambda^{0.5}Q^T$

由于 $\Lambda$ 表示的是特征矩阵，其转置形式等于其本身，因此这里的 $Q=R$, $\Lambda^{0.5} = S$ 且前者恰好为长度为 1 的矩阵后者也恰好是对角矩阵只能放缩向量, 一切都是那么的合理
这一步也说明了高维椭球的各个轴向量来自特征向量 (矩阵) $Q$ 以及各轴长度来自其对应的特征值 ($\Lambda$)

抛掷雪球

这一步主要是说明高斯椭球在进行仿射变换之后其在摄像机坐标系下的投影的形状大小

齐次坐标系

在计算机图形学中往往会用 4 维向量 $\begin{bmatrix} x,y,z,1\end{bmatrix}$ 来表示坐标位置，其中最后一个维度往往用作 平移的效果，即平移矩阵可以将移动量放到 $4\times 4$ 矩阵的最后一列表示各个维度的平移量

正交投影

没有近大远小的局限，是直接进行垂直投影
速度比较快
对一个 长方体 $[l,r]\times [d,u] \times [b,f]$ 进行正交投影通过以下步骤

1. 将中心平移到原点
2. 将长方体缩放至 边长为 2 的正方体 (-1 ~ 1)
   由于是线性变换，可以写成矩阵积：

$M_{ortho} = \begin{bmatrix}\frac{2}{r - l} & 0 & 0 & 0\\ 0 & \frac{2}{u - d} &0 & 0\\ 0 & 0 & \frac{2}{f - b} &0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix}1 & 0 & 0 & -\frac{r + l}{2}\\ 0 & 1 & 0 & -\frac{u +d}{2}\\ 0 & 0 & 1 & -\frac{f+b}{2}\\ 0 & 0 & 0 & 1\end{bmatrix}$

前者表示缩放矩阵，后者表示平移矩阵

透视投影

存在近大远小的局限，需要进行 z 轴距离的放缩
先将投射投影转变成正交投影再进行正交的处理方法, 这里需要涉及对空间的非线性变换 (压缩局部空间), 例如将图中的视锥变成一个长方体形状
假设有非线性压缩变换映射 $m(\cdot)$: 即将任意输入点映射到对应的新空间坐标
高斯球的均值 $\mu_k$ 可以通过映射直接得到 $m(\mu_k)$ , 而其协方差矩阵的变化由于是高维形式向量组，需要额外的变换步骤

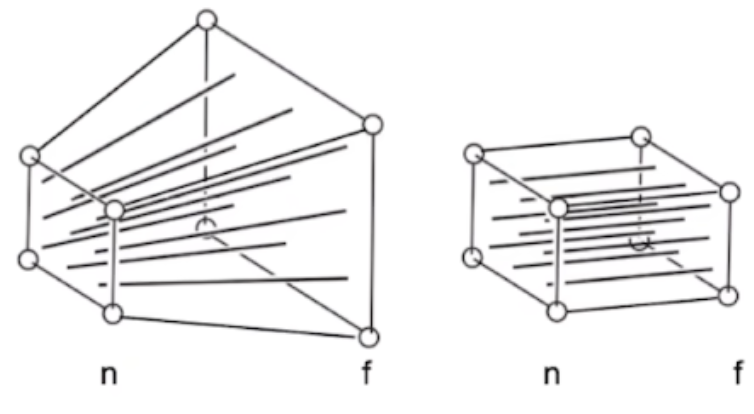
这一步可以用雅各比矩阵来进行变换

雅各比矩阵 jacobian

对于 n 维度空间内每个维度可以表述为 $x_i$, 且一个空间的第 i 维度表面表达式可以写作 $f_i (x_1 ,x_2\cdots)$ 那么对应的 雅各比矩阵的值为

$J = \begin{bmatrix}\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} &\cdots& \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} &\cdots& \frac{\partial f_2}{\partial x_n}\\ \vdots & \vdots &\cdots& \vdots\\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} &\cdots& \frac{\partial f_n}{\partial x_n}\end{bmatrix}$

可以理解为在微元空间下的近似线性空间
因此协方差矩阵的变化为 $\Sigma' = JW\Sigma W^T J^T$ , $J := \frac{\partial m(u_k)}{\partial u}$

合成图像

球谐函数

对于一个球坐标系下的拉普拉斯等式 $\Delta f = 0$, 或者说对于一个标量场内进行梯度 (这一步将标量场变成矢量场) 和散度 (找到一个矢量场的沿着各个维度的矢量导数) 找到为 0 的地方 (即矢量场中场向量完全平行的地方) 这类问题的解在球坐标系下的形式的角度部分就是球谐函数, 即对于偏微分方程

$\Delta f = \frac{1}{r^2}\frac{\partial}{\partial r} (r^2 \frac{\partial f}{\partial r}) + \frac{1}{r^2\sin \theta}\frac{\partial}{\partial \theta}(\sin \theta \frac{\partial f}{\partial \theta}) + \frac{1}{r^2\sin^2 \theta}\frac{\partial^2 f}{\partial \varphi^2} = 0$

将变量分离得到 $f(r,\theta,\phi) = R(r) P(\theta) Y(\varphi)$ 并且将原方程变成

$\frac{r^2 R'' + 2rR'}{R} + \frac{\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}(\sin \theta P')}{P} + \frac{1}{\sin^2\theta}(\frac{E''}{E}) = 0$

由于变量分离之后的每个方程两边必须等于一个常数, 因此令
$E''/E = -m^2$, $\frac{r^2 R'' + 2rR'}{R} = n(n+1)$
那么 $E = c_1 e^{im\phi} + c_2 e^{-im\phi}$ 是一个常见的二阶线性微分方程
$R$ 具有 柯西-欧拉微分方程的特性而解为 $R = c_3 r^n + c_4 r^{-n-1}$
最终 $P$ 可以通过上述方程用 m 和 n 进行表示常数项, 并且从化简上用 $t:= \cos \theta$ 换元得到最终等式

$(1-t^2)P''(t) + 2tP'(t) + (n(n+1)-\frac{m^2}{1-t^2})P = 0$

这个等式符合 连带勒让德函数 (associated Legendre function), 解为 $P_n^m(t) = (1-t^2)^{\frac m2}(\frac{d}{dt})^m P_n(t)$
因此整个方程的解为

$f(r,\theta,\varphi) = (c_1 e^{im\varphi} + c_2 e^{-im\varphi})(c_3 r^n + c_4 r^{-n-1})P_n^m (\cos\theta)$

此时定义球谐函数 $Y_n^m(\theta, \varphi) := N\cdot e^{im\varphi} \cdot P_n^m(\cos\theta)$ 也就是上述公式不考虑 $r$ 径向变量 (或者说令半径恒定为 1) 的结果, N 为归一化常数

为什么用球谐函数

在函数空间中，每个连续的函数都可以表示为基函数的线性组合，而球面函数 (例如球面的某个坐标位置的渲染颜色) 可以表示为球谐函数的线性组合, 其表达式为

$f(t) \approx \tilde {f} = \sum_{n = 0} \sum_{m = -n}^n c_n ^m y^m_n$

其中用到的球谐函数值可以在下表中查找：

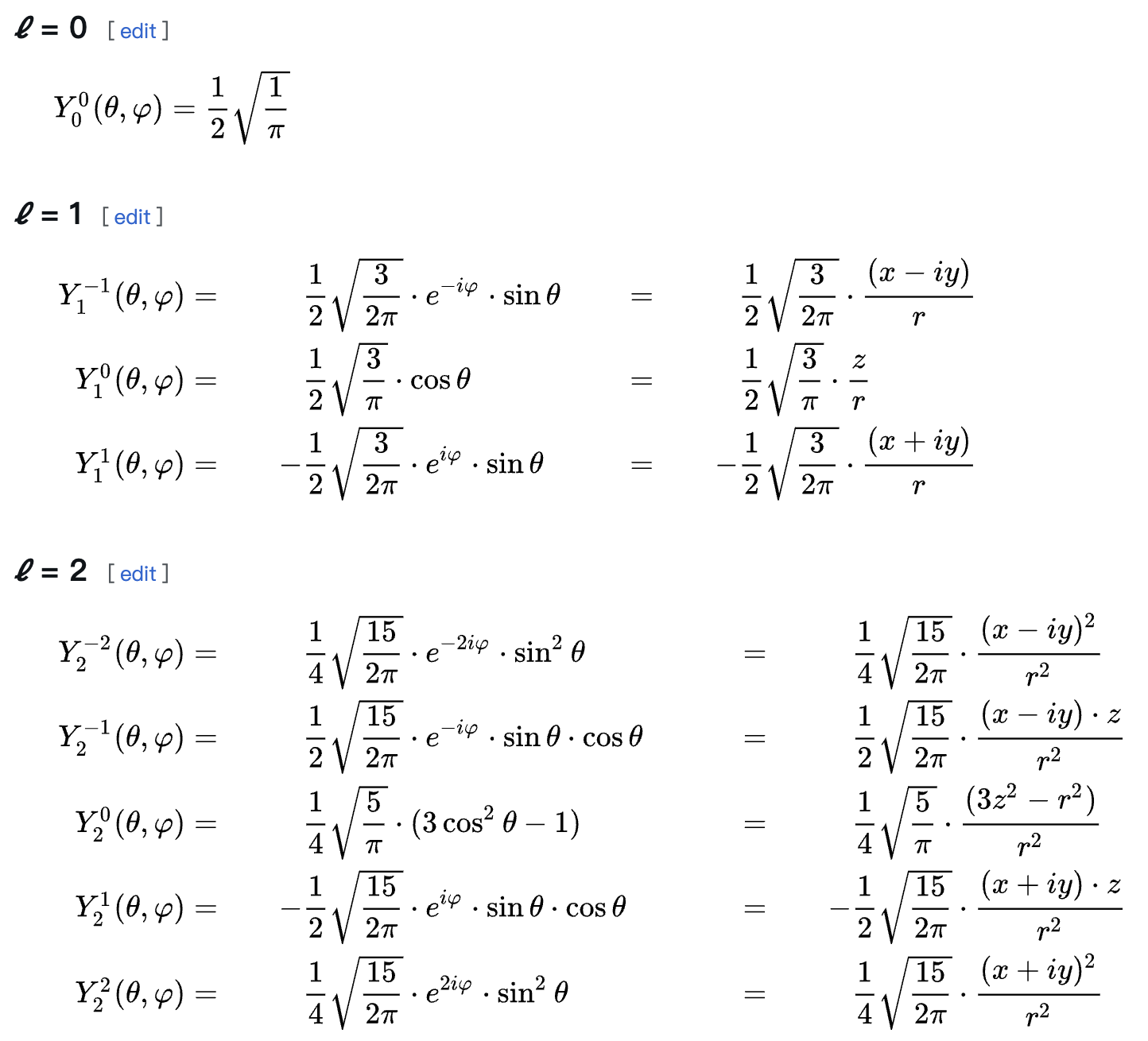
n 和 m 的光学意义

n 表示球谐函数步骤方向信息的精细程度, n 较小的时候可以描述较为光滑的光照变化，n 大的时候可以表述为复杂的方向变化
m 表示方位角的波动和依赖关系
这里引入球谐函数是为了说明在不同角度下看向球会得到不同的颜色

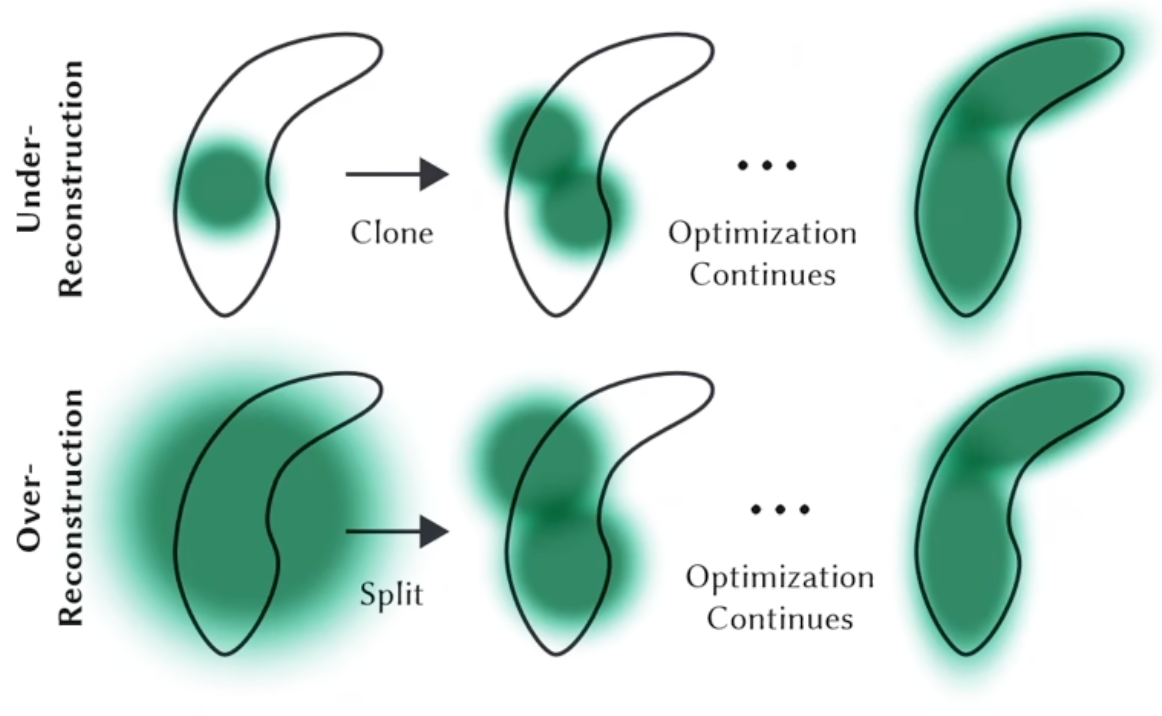
总结

通过点云可创造3D Gaussians(position, covariance matrix, opacity)作为3D表示。color通过球谐函数SH存储