χ2\chi^2 Distribution

卡方分布就是通过 n 个(维) 标准正态随机变量的平方和的分布
对于 Z ∼N(0,1)\sim N(0,1) 的分布 U = Z2Z^2 被称为1自由度卡方分布 (chi-square distribution with 1 degree of freedom) , 写作 χ2(1)\chi^2(1)
定义 U1,U2,⋯UnU_1, U_2,\cdots U_n 是独立卡方分布变量且有一个自由度，那么 分布

V=U1+U2+⋯+Un=χ2(n)V = U_1 + U_2 + \cdots + U_n = \chi^2(n)

就拥有chi-square distribution with n degrees of freedom
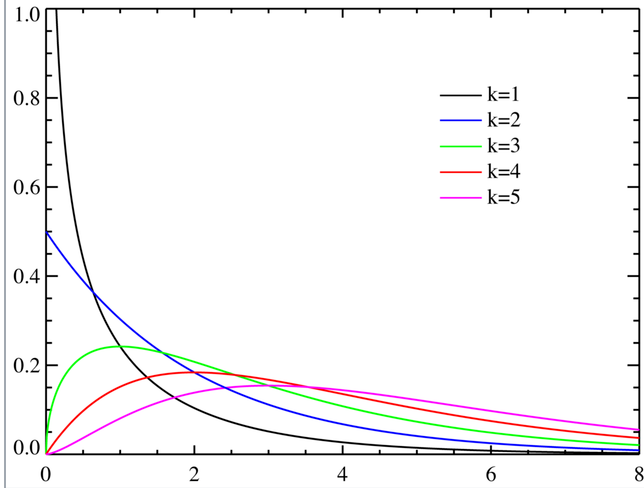
chi-square.png

从 Gamma 函数到卡方分布

注意到，欧拉 gamma 函数的参数 α=n2,β=2\alpha = \frac{n}{2}, \beta = 2 的情况就是卡方分布的函数 χ2(n)\chi^2(n)
由于原随机变量 XX 满足正态分布的特征，因此其分布函数为 fX(x)=12πe−x22f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} 那么换元成 χ(1)\chi(1) 就是 fχ(χ)=12πe−χ/2χ−12f_\chi(\chi) = \frac{1}{\sqrt{2\pi}} e^{-\chi/2} \chi ^ {-\frac{1}{2}}

描述目的

由于 χ2\chi^2 相当于是对 N(0,1)N(0,1) 的随机变量的的平方分布进行研究，可以简单理解为方差的分布，在统计中往往用来估计数据的离散程度
单个自由度卡方分布是右偏的 (skewed to the right)，它的形状类似一个长尾分布，表明在零附近的概率较高，但仍然存在较大的正数取值的可能性

常用 pivotal 形式

χ2(n−1)=(n−1)S2σ2\chi^2(n-1) = \frac{(n-1) S^2}{\sigma^2}

这里的 S2S^2 表示样本的方差，表达式是 1n−1∑in(Xi−X‾)2\frac{1}{n-1} \sum_i^n (X_i - \overline X)^2 那么右表达式就是 χ2(n−1)=∑(Xi−X‾σ)2=∑Zi2\chi^2(n-1) = \sum(\frac{X_i - \overline X}{\sigma})^2 = \sum Z_i^2 就是标准的分布
卡方分布的自由度为 n - 1 是因为样本方差的计算涉及到样本均值 Xˉ\bar{X}，这消耗了一个自由度
χ2\chi^2 常用于估计 σ\sigma 的数值

t 分布 (学生分布)

t 分布描述了样本量较小 (n < 30) 的情况下样本均值离总体均值的距离
定义 Z∼N(0,1)Z\sim N(0,1) 与 U∼χ2(n)U\sim \chi^2(n) 且 Z,U 之间独立, 那么随机变量 T:=ZU/nT:=\frac{Z}{\sqrt{U/n}} 的分布为 t distribution with n degrees of freedom
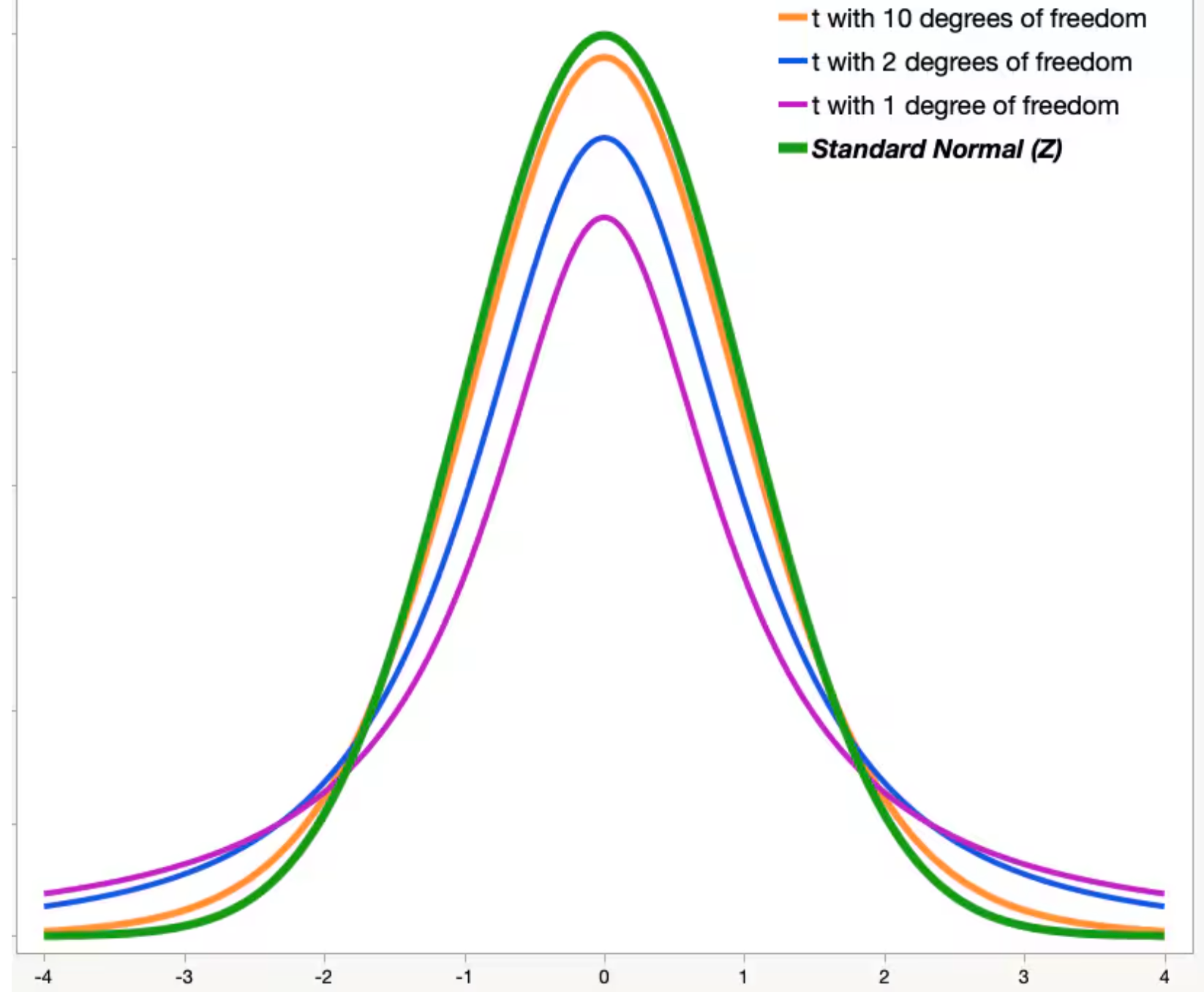
t_distribution.png
简单观察这个函数的形式，其即为 Z 值除以了一个 U/n\sqrt{U/n} 即一个类似标准化用的因数 这个数也可以理解为 σ2/n\sqrt{\sigma^2 /n} 的一个变量, 也就是一个类似平均标准差的东西但是往往会小于 1 (因为 U 本身是一个类似 σ=1\sigma = 1 的分布) 因此在样本数较小的时候其会增大尾部的分布情况，增大了不确定性
t 分布也是以自由度为变量的函数(两个输入 T 和 n) 其分布形状接近于一个 bell curve, 但是中间会低于 normal ，两边会高于 normal, 当且仅当 n→∞n\to \infty 的时候 bell curve 会接近于 normal

常见 pivotal 形式

T=X‾−μS/n∼t(n−1)T = \frac{\overline X - \mu}{S / \sqrt{n}} \sim t(n-1)

把 SS 变成全局标准差就是 Z 了
自由度为  n - 1  的原因主要与样本方差  S^2  的计算有关。由于我们需要用样本数据估计总体方差，而样本方差的计算涉及到样本均值 Xˉ\bar{X}，这消耗了一个自由度
T 分布常用来作为 σ\sigma 未知或者样本量小于 30 情况下估计 μ\mu 的枢纽量

F 分布

F 分布通过两个独立的卡方分布的比值构建，主要用于描述两组数据的方差之间的相对差异
对于两个卡方分布 X∼χ(m)X\sim \chi(m), Y∼χ(n)Y\sim \chi(n) 那么其表达式为 F(m,n)=X/mY/nF(m,n) = \frac{X/m}{Y/n}

  • 非对称性：F 分布是一种右偏分布，形状类似于长尾分布。随着 m 和 n 的变化，F 分布的形状会有所变化。
  • 自由度的影响：F 分布的形状由自由度 m 和 n 决定。通常，m 是与分子卡方变量相关的自由度，n 是与分母卡方变量相关的自由度。随着 m 和 n 的增加，F 分布逐渐趋近于对称分布。
  • 均值和方差：当 n > 2  时，F 分布的期望为 nn−2\frac{n}{n - 2} ；当 n>4n > 4 时，方差存在，其计算公式为 2n2(m+n−2)m(n−2)2(n−4)\frac{2 n^2 (m + n - 2)}{m (n - 2)^2 (n - 4)} 。
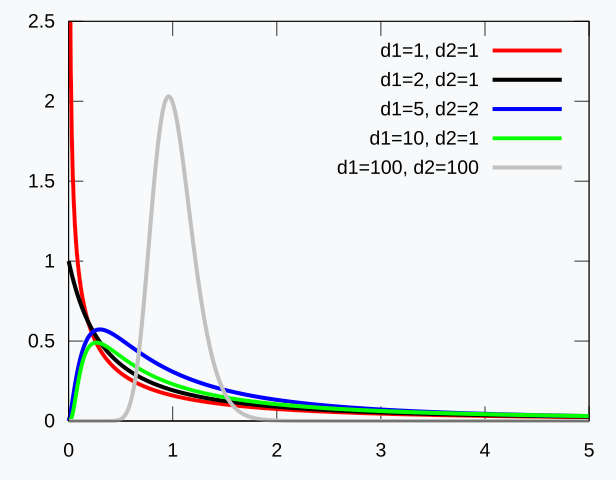
    F-distribution.png
    注意在自由度较高的时候, 其图像会达到在 x=1 的时候的情况达到最大

常用 pivotal value

一般用变量 F=(sX/sY)2(σX/σY)2∼F(nX−1,nY−1)F = \frac{(s_X / s_Y)^2}{(\sigma_X/\sigma_Y)^2}\sim F(n_X - 1, n_Y - 1) 作为 pivotal quantity
这里由于在计算 ss 的时候会用到样本参数 Xˉ,Yˉ\bar X, \bar Y 因此两个随机变量的自由度分别降低一次
F 常用于估计两个 标准差比值的枢纽量

几个定理

对于独立同分布随机变量 X1,X2⋯Xn∼N(μ,σ)X_1, X_2 \cdots X_n \sim N(\mu, \sigma)
Theorem1: X‾\overline X 与 S2S^2 independent
Theorem2: (n−1)S2σ2∼χ2(n−1)\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1)