4. Cook-Levin Theorem

定理内容

SAT 问题是 NP-complete 问题
由于 SAT 问题在给定 certificate 的情况下只需要逐个检验是否符合, 复杂度是 polynomial -> NP, 因此这里只需要证明其是 NP-hard 即可

证明 NP-Hard

利用 NP-hard 的定义, 这里需要证明对所有的 language $L\in NP$ 都有 $L\le_p SAT$ (因为 SAT 问题往往会作为 NP-hard origin 来归纳其他的问题是否 NP-hard, 这里不能用其他 NP-hard 来归纳之)
因此假设我们有一个任意 np 问题的 instance x 和一个输入语言 L $\in$ NP, 即存在 $Verify-L$ 可以在多项式时间内决定 L;
证明目的是是否存在一个 SAT instance $\phi$ satisfiable iff 存在 c 使得 Verify-L(x,c) accept
定义 VL 算法为一个 TM, 并将其编码为一个 $|x|^k\times |x|^k$ 的一个表格 tableau of Verify-L(x,c)
表格的每一行表示图灵机执行了一步, 其中每个元素是 x 的值 alphabet 或者 c 的 alphabet 或者 TM 的状态 $q_i$ 以及 $\bot$

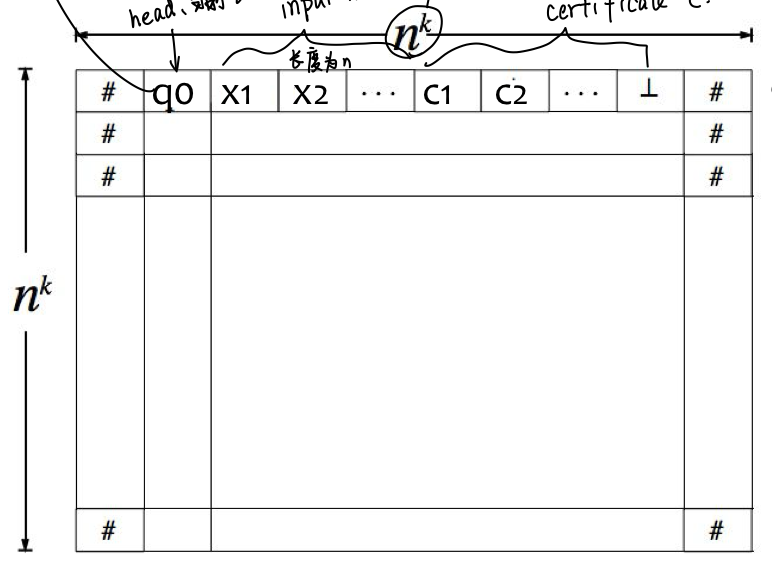
定义存在性函数 $t_{i,j,s} = \{T,F\}$ 表示在表格 i 行 j 列位置上是否数值为 s
定义 clause $\phi$ 为部分 t 的表达式子的 and / or 逻辑结果, 那么可以将这个 TM 是否有解转变为满足几个条件
那么利用这个定义可以将证明目的变成 construct instance $\phi$ satisfiable iff 存在 c 使得 tableau of VL contains $q_{accept}$

逻辑转换

在这里可以将 instance (tableau) 变成几个子逻辑取 and 逻辑即

$\phi = \phi_{start} \land \phi_{cell} \land \phi_{accept} \land \phi_{step}$

• $\phi_{start}$: 定义了第一行的输入限制
  • $\phi_{start} = t_{1,1,wall}\land t_{1,2,x_1} \cdots \land t_{1, n+2, x_n} \land t_{1,n+3,\$}, \land (t_{1,n+4,0}\lor t_{1,n+4,1}\lor t_{1,n+4,\bot})\cdots$
• $\phi_{cell}$: 定义了每个 cell 只能有一个元素
  • $\phi_{cell} = \bigwedge_{1\le i,j\le |x|^k} (\bigvee_s t_{i,j,s}\land \neg(\bigvee_{s\neq s'} (t_{i,j,s}\land t_{i,j,s'})))$
• $\phi_{accept}$: 存在一个 $q_{accept}$
  • $\phi_{acc} = \bigvee_{1\le i,j\le |x|^k } t_{i,j,q_{acc}}$
• $\phi_{step}$: 保证每一行来自前一行
  • 构造一个 $2\times 3$ 的格子，满足上一层和下一层的 q 都在各自内且遵循图灵机的格式进行变换，那么每次的这个格子都能写成 6 个 t 的 and

$(\Leftarrow)$ 证明思路

既然存在 c 使得 $VL(x,c)$ accept, 那就说明表格中存在 $q_{accept}$, 那么就会有对应的 $\phi$ 使得 SAT 问题成立 (因为存在c所以会有对应的表格存在, 因此其四个clause必然能满足)

$(\Rightarrow)$ 证明思路

当 $\phi$ 返回 yes 说明存在一个赋值可能性使得其 satisfy, 那么就是上述四个 cluase 同时满足 那么就会对于各个格子的状态 t 存在一定的约束条件，因此存在格子的赋值方法使得 certificate 可解 (因为有 accept 存在) 且上述逻辑保证了一个合理的图灵机处理过程的结果, 因此结果可信