1. 贝尔曼公式

决定形式

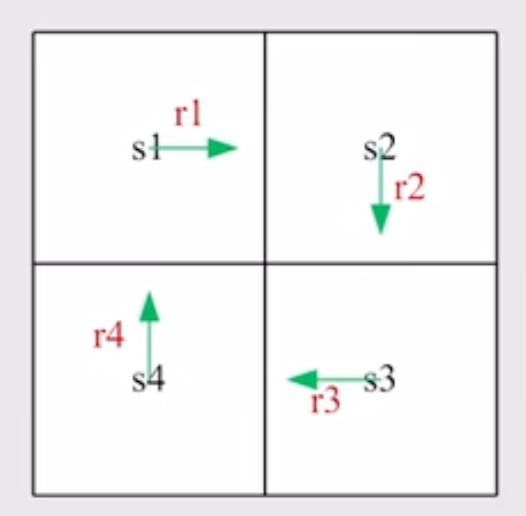
假设有一个 $2\times 2$ 的 grid 网格，一个程序会分别从四个节点出发沿着顺时针方向旋转, 返回值分别为 $v_1, v_2, v_3, v_4$ 那么每个值分别可以表述为

$v_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + \gamma^3 r_4 + \cdots$

类似的可以写出 $v_2, v_3, v_4$ 的表达式
将 $v_1$ 表达式进行变化得到递归形式:

$v_1 = r_1 + \gamma(r_2 + \gamma r_3 + \cdots) = r_1 + \gamma v_2$

这一步被称为 bootstrapping. 同理这也可以写出 $v_2, v_3, v_4$ 的表达式，同时我们可以用向量和矩阵来进行表示

$\vec v = \vec r + \gamma P \vec v$

其中， $\vec v = \begin{bmatrix}v_1\\v_2\\v_3\\v_4\end{bmatrix}$ $\vec r = \begin{bmatrix} r_1\\r_2\\r_3\\r_4\end{bmatrix}$ $P = \begin{bmatrix}0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\end{bmatrix}$ (这里仅限于可定action 的 bellman function)

state value

terminology

$S_t\overset{A_t}{\rightarrow} R_{t+1}, S_{t+1}$

• t: discrete time instance
• $S_t$: state at time t
• $A_t$: action taken at state $S_t$
• $S_{t+1}$: the state transited to after taking $A_t$
  Discounted Return: $G_t = R_{t+1} + \gamma R_{t+2} + \cdots$
  以上的 $S_t, A_t, G_t$ 都是 random variable

state value 的定义

state value 表示的是 $G_t$ 的期望值

$v_\pi (s) = \mathbb{E}[G_t | S_t = s]$

这是一个关于 s 的函数, 表示的是从 state start at s 的获得 return
值的期望, 使用的策略用对应的 $\pi$ 进行表示
如果对于不同的策略其获得的 $v_\pi(s)$ 越大说明其效果越好, 该方法可以被 preferred

state value 和 return 的区别

state value 是各种可能的 return 的平均值水平, 但是如果每一步都是 deterministic 可以直接决定的, 那么 state value 和 return 值相等了 (因为其他的可能性为 0, 不会改变期望)

用 BM 公式求解 state value

首先展开 return 的表达式得到递推形式:

\begin{align*} G_t = & R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots\\ = & R_{t+1} + \gamma(R_{t+2} + \gamma R_{t+3} + \cdots)\\ = & R_{t+1} + \gamma G_{t+1} \end{align*}

那么改写标准 state value 的公式可以得到(利用期望的线性特征):

\begin{align*} v_\pi(s) = & \mathbb{E}[G_t | S_t = s]\\ = & \mathbb E [R_{t+1} + \gamma G_{t+1}|S_{t} =s ]\\ = & \mathbb E[R_{t+1} | S_t = s] + \gamma E[G_{t+1} | S_t = s] \end{align*}

分别展开两项公式，对于左边那个可以得到:

\begin{align*} \mathbb E[R_{t+1} | S_t = s] =& \sum_{a} \pi (a | s) \mathbb E [R_{t+1} | S_t = s, A_t = a]\\ =& \sum_a \pi(a| s)\sum_r p(r | s,a) r \end{align*}

也就是说利用全概率公式将当前期望分成不同 action 的期望的求和, 且最后展开得到了当前 state 的各个 action 的加权求和, 这是一个 immediate reward, 常用 $r_\pi (s)$ 表示
后面那个部分，也是利用全概率公式展开：

\begin{align*} \mathbb E[G_{t+1} | S_t = s] =& \sum_{s'}\mathbb{E} [G_{t+1} | S_t = s, S_{t+1} = s']p(s'|s)\\ = &\sum_{s'} \mathbb{E}[G_{t+1} | S_{t+1} = s'] p(s' | s)\\ = & \sum_{s'} v_{\pi} (s')p(s'|s)\\ = & \sum_{s'} v_{\pi}(s')\sum_a p(s'| s,a)\pi(a | s) \end{align*}

注意这里的第一步到第二步的变换用到的是 马尔可夫过程的假设，即在知道 $S_{t+1}$ 的情况下不考虑前面的 state (可以理解为后面的 state 事实上包含了前面 state 的概率信息)
这个表达式表述了来自未来的 reward 值总和, 常用 $p_\pi(s' | s) = \sum_a \pi(a | s) p(s'|s, a)$ 进行表示
再将上两个子式提出得到标准的 贝尔曼函数

$v_\pi(s) = \sum_a\pi(a | s)[\sum_rp(r | s,a) r + \gamma \sum_{s'}p(s' | s,a)v_\pi(s')]$

再利用上文提到的 bootstrapping 的方法, 将所有的 state 对应的等式列出来, 我们可以得到一组线性方程组, 为了方便向量和矩阵的书写格式，我们可以采用上面提到的两个简化子进行公示优化

$v_\pi(s_i) = r_\pi(s_i) + \gamma \sum_{s_j}p_\pi(s_j | s_i) v_\pi(s_j)$

写成线性表达式就是

$v_\pi = r_\pi + \gamma P_\pi v_\pi$

• $v_\pi = [v_\pi(s_1),v_\pi(s_2),\cdots, v_\pi(s_n) ]^T$
• $r_\pi = [r_\pi(s_1), r_\pi(s_2),\cdots, r_\pi(s_n)]^T$
• $(P_\pi)_{ij} = p_\pi(s_j | s_i)$

求解 BM

直接对矩阵求逆的过程过于复杂了，这里往往采用 迭代法
利用递推表达式 $v_{k+1} = r_\pi + \gamma P_\pi + v_k$ 的公式，证明在 $k\to\infty$ 的时候 $v_k\to v_\pi$
这个类似于一个 概率矩阵的 特征值严格小于1从而会不断压缩映射空间向不动点靠近最终收敛
不过这同理也说明了设定的初始值 $v_0$ 的数值并不是那么重要

Action Value 执行价值

action value 表示的是在给定 state 下执行某个 action 获得的期望 return
相比于 state value, action value 更能说明一个决策步骤的收益

定义式

$q_\pi(s,a) = \mathbb E[G_t | S_t = s, A_t = a]$

与 state 的联系

$v_\pi(s) = \sum_a q_\pi(s,a) \pi(a|s)$

注意联系状态和执行的为 policy 函数, 以条件概率的形式出现
说明状态价值函数是 行为价值函数的策略期望
这个公式在形式上和前面所说的 state 线性函数形式非常像，即：

$q_\pi(s,a) = \sum_r p(r|s,a)r + + \sum_{s'} p(s' | s,a) v_\pi(s')$

这个公式的好处就是方便用 state value 去求解 行为价值函数