树的定义

  1. 没有 cycle 的无向图
  2. rooted tree
    1. 存在某个 node 作为根节点
    2. 每个节点事实上都可以作为 root

二叉树的操作复杂度

二叉树的方法时间复杂度看的主要是二叉树自身的结构形状，如果是 complete 树是最好情况; 如果是 每个节点都只有一个子枝，其复杂度最大，是 worst case

数组法

  1. insert
    1. 最好 O(1)
    2. 最差 O(n)
    3. 和树的排布方式有关，如果树的根节点的某个字节点为空那么直接插入，复杂度 O(1); 如果全部排满我们需要遍历找到空节点位置那么时间复杂度 O(n)
  2. remove
    1. 最差 O(n)
  3. parent O(1)
  4. child O(1)
  5. space
    1. 最好 O(n)
    2. 最差 O(2^n)
    3. 这里取决于数据的排布方式, 如果是完全二叉树，那只需要 O(n) 空间; 如果是完全一叉树 (每个node最多只有一个节点) 就需要 O(2^n) 空间

指针法

  1. insert 好 O(1) 坏 O(n)
  2. remove 坏 O(n)
  3. parent O(n) 因为没有爹指针
  4. child O(1)
  5. space 好 O(n) 坏 O(n)

遍历方向 ordering

preorder

满足 中左右 的顺序

inorder

满足 左中右 的顺序

postorder

满足 左右中 的顺序

查找到BST

一维数组中往往会通过排序来方便查找以及插入，那么二叉树中是否就可以通过类似的排序方法进行查找某一些指定元素呢？
定义二叉搜索树 binary search tree (BST) 满足以下两个 invariant：

  • 当前 node 的数值 大于左子树的 key 值
  • 当前 node 的数值小于等于右子树的key 值
    • 从等于的特性可以发现，等于当前 node key 值的节点的位置一般在右子树的最左侧子枝
      对于这样的树，其查找的复杂度：O(height)O(\text{height}) 注意不能简单的定义为 O(log⁡n)O(\log n) 因为对于非完整树其高度不能定义为 O(log⁡n)O(\log n)

对于给定数据集构造最好树和最差树

最好树就是 complete 树
最差树形状是 单调递增/单调递减/z字形，即每一步要么选当前最大要么选 当前最小, 因此其可能性数量是 2n−12^{n-1}

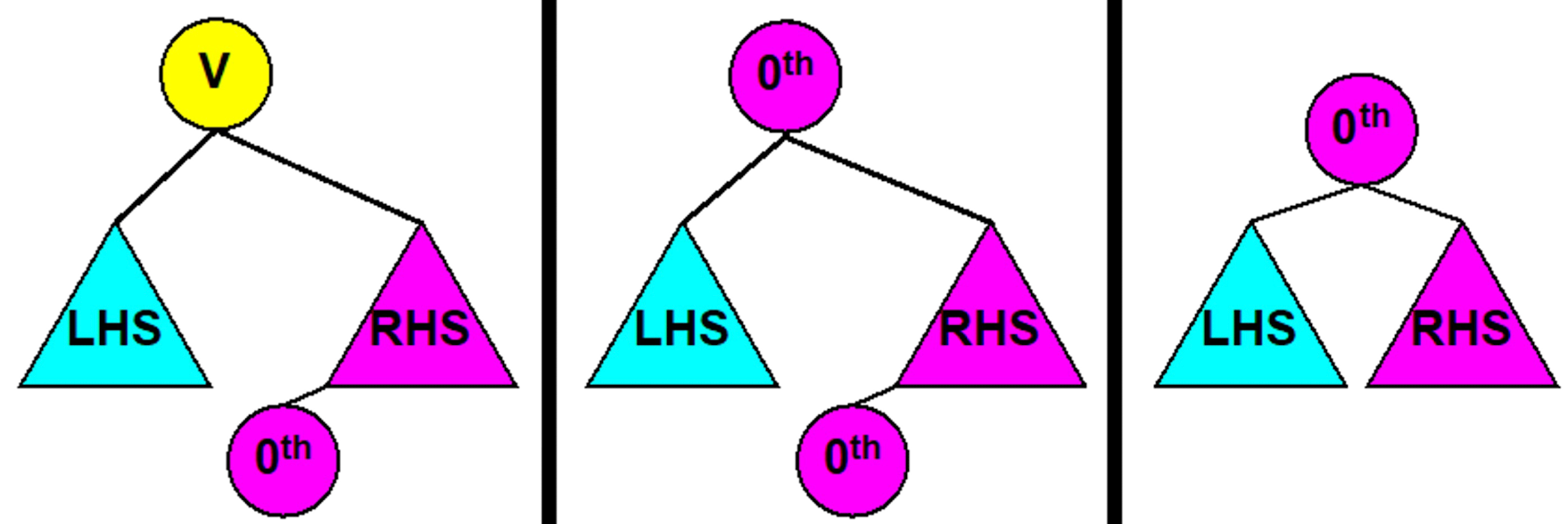
remove 方法的实现

假设删除的元素是某一个根节点且该节点有左右子树，那么需要 keep the invariance, 需要将一个大于左子树所有元素且小于等于右子树所有元素的值放到根节点上。从左子树考虑，这个元素只能位于最右侧子枝; 同理从右子树考虑这个元素只能位于最左侧子枝; 但是根据惯例使用右边的更多
bst_remove.png

AVL 树

一种自平衡的二叉搜索树, 相比于一般的二叉树加入了 高度自平衡机制 (Height Balance Property)

  • 自平衡: 左右子树的高度差不大于 1
  • 利用 rotation 来进行高度平衡
  • insert/search 的最差时间复杂度是 O(log⁡n)O(\log n)

构成高为 h 的 avl 树的最少节点数量

对于 h > 1, 一个 avl 树的高度 h 包括了: 根节点 + 1个高为 h-1 的左子树和一个高为 h-2 的右子树
所以节点数量的递归关系为 n(h)=n(h−1)+n(h−2)n(h) = n(h - 1) + n(h -2)
且最小节点数 n(h−1)>n(h−2)n(h-1) > n(h-2) 所以有 n(h)>2n(h−2)n(h) > 2n(h-2) 再用递推展开得到 n(h)>2in(h−2i)⇒n(h)>2h/2−1n(h) > 2^i n(h - 2i)\Rightarrow n(h) > 2^{h/2 - 1} 再转变为 log 关系得到 h<2log⁡n(h)+2h < 2\log n(h) + 2
所以 avl 树的高度是 O(log⁡n)O(\log n)

avl 树的排序

插入过程每个只需要 O(log n) 的时间复杂度，因此总复杂度是 O(nlog n)
最终有序数组通过 中序遍历展开

平衡因子 balance factor

balance(n) = height(n->left) - height(n->right)
只能处于 0-1

旋转 rotation

如下图所示，avl 的执行就是交换父子关系，但是保持 bst 的基本性质不变
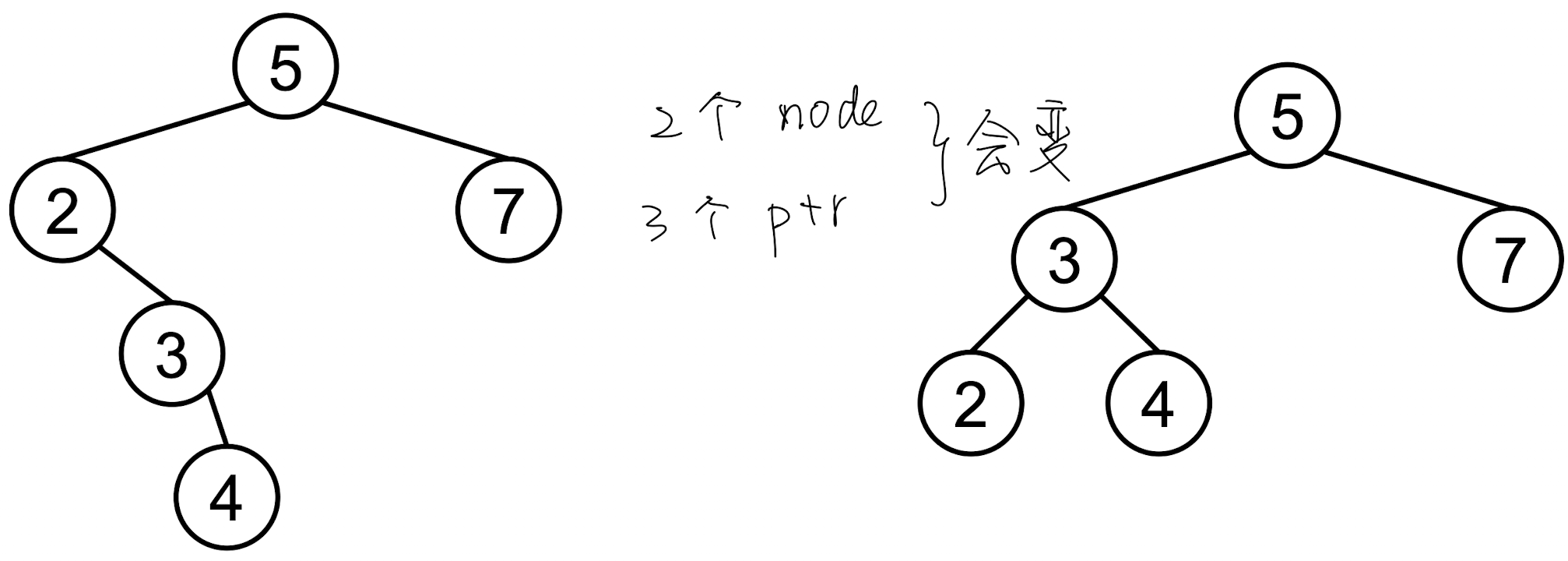
avl_rotation
如上图所示，发生变化的元素有：
2 node: node 2 和 node 3
3 ptr: node2 -> right, node3->left, node5->left
因此每次旋转只会发生常数次变化，复杂度 O(1)O(1)
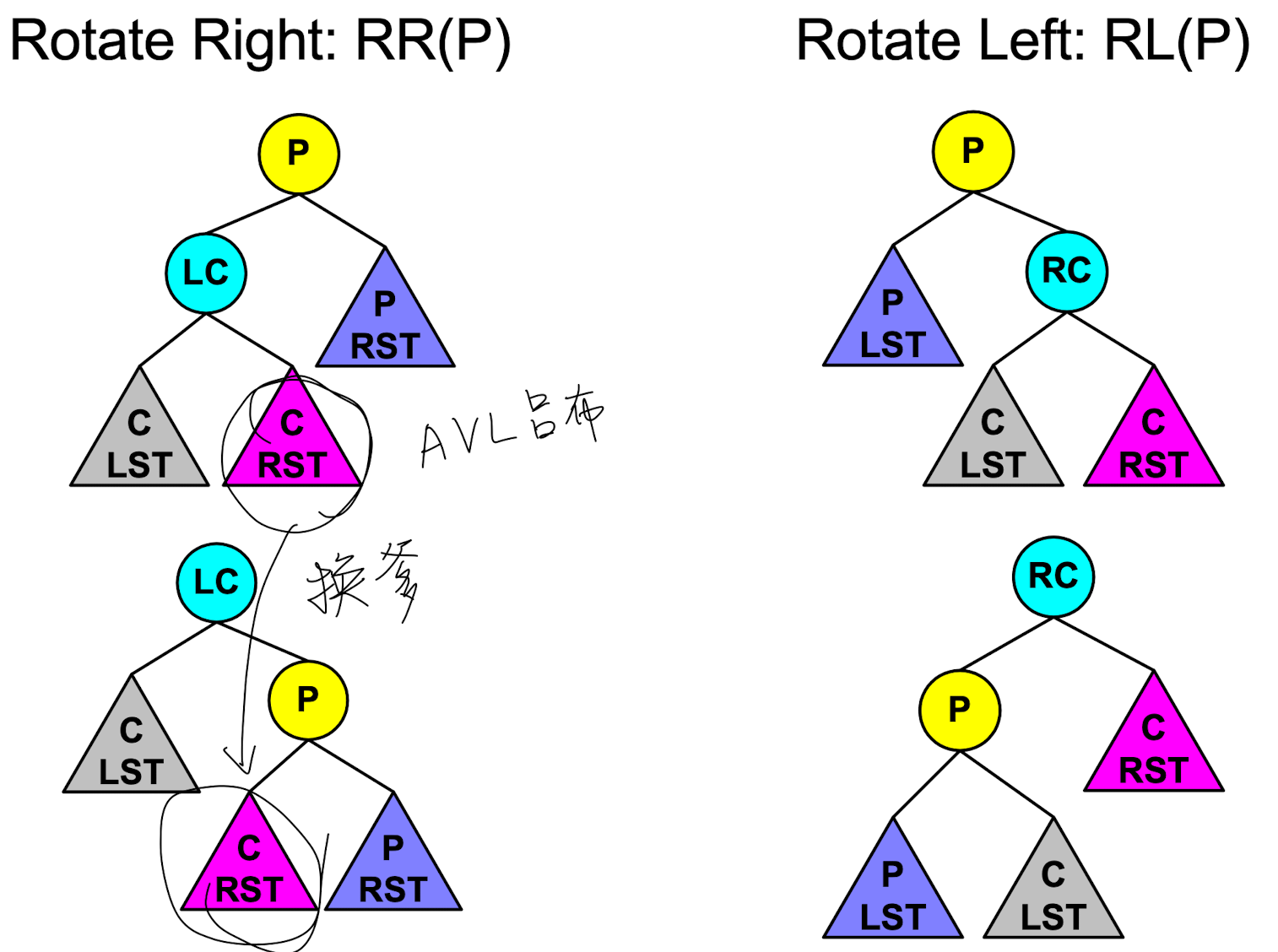
avl_rotation.png

旋转的过程可以分为两类: 左旋RL和右旋RR，定义左旋为父-右子发生交换父子关系; 右旋为父-左子发生交换父子关系 (这里的方向是反的) 且一般描述方向会带有目标节点作为 父节点

插入过程要用到的 旋转

一共有四种可能: RL, RR, RR + RL, RL + RR
那么