定义

总体分布函数完全未知或只知形式不知参数情况下，推断总体某些特性，提出某些关于整体的假设，根据样本对所提出的假设作出接受或是拒绝的决策

假设思路

有两种假设: 零假设和备择假设, 证明思路是将目标论点作为备择假设，定义补集为零假设，通过积分证明零假设不成立，从而证明备择假设(证明目的)成立

两类决策错误

第一类决策错误

弃真错误: H0H_0 为真的时候拒绝 H0H_0

第二类决策错误

取伪错误: H0H_0 不为真的时候接受 H0H_0

零假设的错误可能

如果用假设检验的思路，只会说明 reject H0H_0 或者 not reject H0H_0, 那么我们只有可能会犯弃真错误而不会犯第二类错误，而第一类错误我们可以用一个变量来进行描述

显著性水平 α\alpha significance level

当原假设实际上正确时, 检验统计量落在拒绝域的概率, 就是犯弃真错误的概率
在正态分布的cdf积分表中属于是积分结果一类
significance_level.png

P-value

描述了当前样本在零假设前提下更加极端的概率和，也就是不符合零假设的概率大小

  • 如果 p-val 越大，说明更极端的可能性很大，说明当前取的数值处在合理区间内
  • 如果 p-val 很小，说明没有什么更极端的情况了，说明样本数值不合理
    判断 p-val 大小的阈值就是 显著性水平，也就是用 c.d.f 和 α\alpha 进行比较

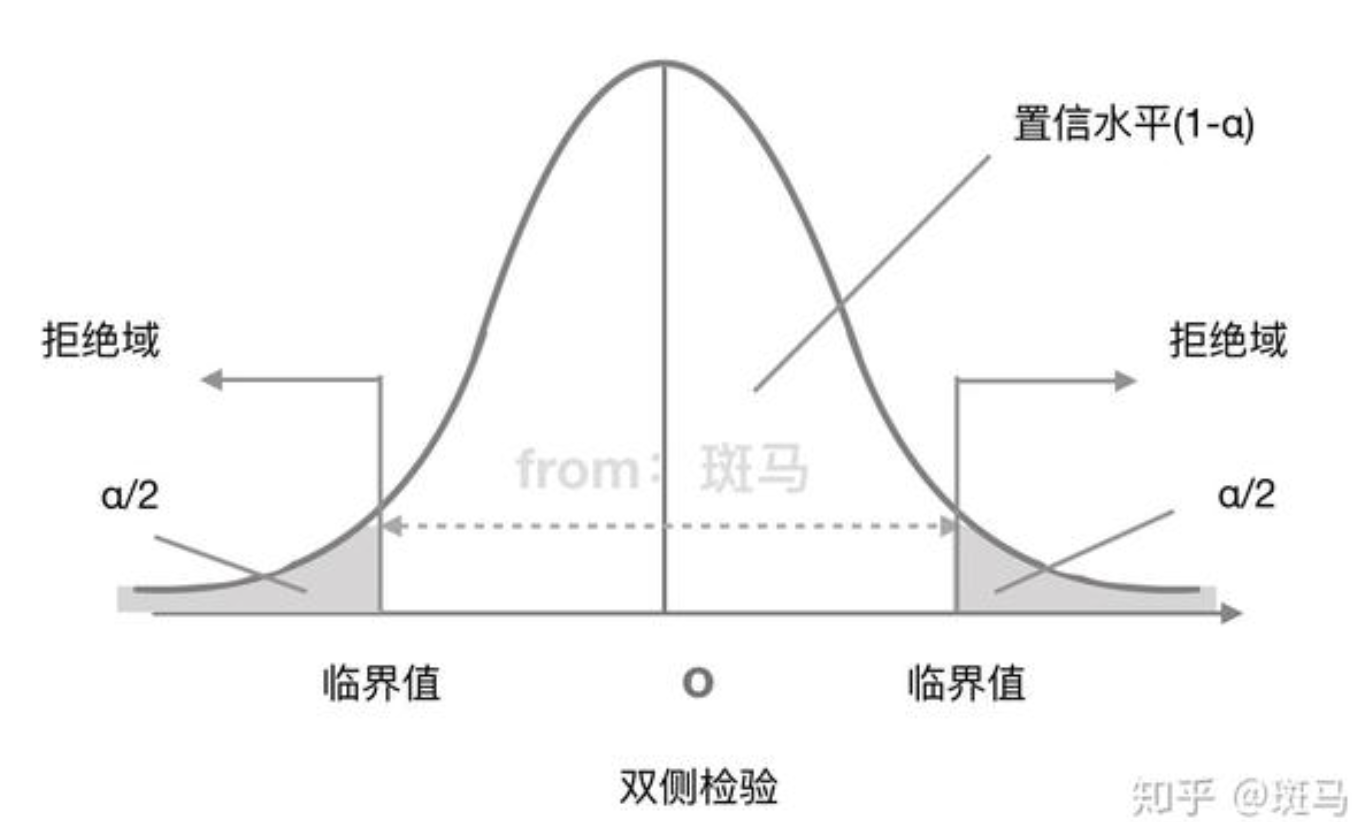
两侧检验和单侧检验

基于 null hypo 的内容可以将检验方向性分为两类
null hypo : X = … 那么检验就是两侧检验
null hypo : X >= … / X <= … 那么检验就是 单侧检验
如果在两侧检验的情况下，通过单向积分得到的概率结果实际上需要乘以二才是标准 p-val, 因为当前样本只能代表一侧的偏离程度

Z-test

对平均值进行估计的时候需要判断样本平均值是否具有特殊随机性还是具有普适性

3 个要求

  1. 样本 X1,⋯ ,XnX_1, \cdots ,X_n independent
    1. 即要求这个样本尺寸占全尺寸的比例不大于 5%5\%
  2. X∼X \sim Normal(μ,σ\mu, \sigma)
  3. σ\sigma 已知 (否则无法计算 σ\sigma)

例

想知道一个年级中某个班级的学生成绩水平，首先用抽样，在这个班中选择 10 个人进行成绩估算，那么要检验这个成绩是否是随机结果还是具有普遍性. 假设我们已经知道年级平均水平 μ\mu 以及标准差 σ\sigma 且成绩符合正态分布, 那么我们可以计算

Z=X‾−μσ/10Z = \frac{\overline{X} - \mu }{\sigma / \sqrt{10}}

然后对比这个和通过 α\alpha 查表计算得到的临界 ZαZ_\alpha 看二者谁更加极端，从而判断当前样本的平均值是否非常极端，如果更加极端，说明采样结果过于偏离，具有随机性，不可信

置信区间 confidence intervals

从同一总体中重复抽样许多次，其中大约 (1−α)100%(1-\alpha)100\% 的样本的置信区间将包含总体的真实参数值 true value (要求这些抽样的分布一致，且样本是随机的、尺寸一致)

参数的置信区间估计

一般利用样本空间来估计 population 的属性, 这些属性往往以定量形式参数 β\beta 等存在.
样本空间是