三门问题

游戏规则

有三个门，只有一个门后面有车，另外两扇门后面是羊，主持人知道哪扇门后面是车或者羊，参赛者不知道。参赛者先选择一扇门，然后主持人打开一扇门，露出一只羊。参赛者可以选择是否换门，然后打开最终选择的门，如果是车则获胜。

问题

参赛者是否应该换门？

解答

如果不改变决策，那么我们看不看到新的信息对于结果没有影响，所以中奖的概率是 1/31/3
如果改变决策，我们就会有几种可能
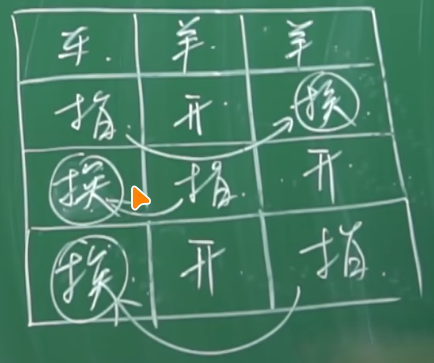
three_door.png
枚举之后，我们会发现在三种情况中，有两种情况是中奖的，所以中奖的概率是 2/32/3
因此我们应该换门

解释

在不知道条件之前，我们选中车的概率是 1/3, 但是在打开一扇门之后，其实我们换门如果成功说明本来就是羊, 这个概率是 2/3
这个例子说明了 信息的获取是可以改变概率空间的结果的

条件约束 Condition

很多随机事件的发生是需要一定条件作为背景的，比如我们讨论 eStar 作为A2获得夏季赛总冠军的概率和 eStar 在夏季赛决赛中获得总冠军的概率必然是不同的，后者多了一个条件: eStar 进入到夏季赛决赛
我们令事件 A:=A: = eStar 获得夏季赛总冠军, B:=B: = eStar 进入到夏季赛决赛, C:=C:= eStar 夏季赛决赛后获得夏季赛总冠军
那么我们可以得到:

P(A) = P(B) \times P(C)$$ 或者说 $P(A) = P(B\cap C)$ 当然我们也可以认为，eStar 获得冠军的概率等于其 进入决赛的前提下获得冠军的概率 乘以 进入决赛的概率，定义 $|$ 为条件符号，则: $$ P(B\cap C) = P(C|B) \times P(B)

这就是条件概率的定义

条件空间有什么用？

从上面两种相似的公式我们可以看出来，条件概率和并集的化简有很大关系，我们前一课学过的并集可以拆分成两个概率的乘积，但是这个需要两个事件相互独立（这个定义后面会用数学公式说明）的前提；然而，如果并不独立，我们就要用条件概率进行拆分化简了
例如对于概率 P(B)P(B) 我们可以写作 P(B∣A1∪A2)P(B | A_1\cup A_2) 即达成 B 的条件必须有 A_1 和 A_2 两个前提; 比如 B:= eStar 进入败者组决赛, A_1:= eStar 击败 狼, A_2:= eStar 击败 AG
在直接写 P(B) 的时候背景就决定了只有这两种可能，因此我们朴素的可以理解为

P(B∣A1∪A2)=P(B∣A1)×P(A1)+P(B∣A2)×P(A2)P(B|A_1\cup A_2) = P(B|A_1) \times P(A_1) + P(B|A_2) \times P(A_2)

细节的定义会在后面 (注意这里 A_1, A_2 互斥)
条件空间的存在很好的划分了概率空间，在已知条件概率的时候能够有效转变不同信息带来的概率变化

条件空间下的补集

P(A∣B)=1−P(Ac∣B)P(A | B) = 1 - P(A^c | B)

独立事件

对于两个事件，如果 P(A|B) = P(A), 那么称事件 A 与事件 B 独立
简单来说，就是事件 B 的发生不会影响事件 A 的发生概率，比如 WB 与 LGD 的比赛结果，不会影响 eStar 与 EDGM 的比赛结果

多元独立事件

如果有多个事件，如何判断三者两两独立？
定义 P(A)=P(A∣B)=P(A∣C)=P(A∣B∩C)P(A) = P(A | B) = P(A | C) = P(A | B \cap C)

全概率公式 Law of Total Probability LTP

如果两个事件之间并不相互独立，且我们需要化简 P(B∩C)P(B\cap C) 就必须使用全概率公式

P(B∩C)=∑iP(B ∣ Ci​)×P(Ci​)P(B\cap C)=\sum_i P(B\ |\ C_i​)\times P(C_i​)

贝叶斯定理 Bayes’ Rule

如果我们要更换条件给定的顺序，那么我们就有

P(A ∣ B)=P(B ∣ A)×P(A)P(B)P(A\ |\ B) = \frac{P(B\ |\ A) \times P(A)}{P(B)}

再用全概率公式展开，可以写作

P(Ak ∣ B)=P(Ak∩B)P(B)=P(B ∣ Ak)×P(Ak)∑iP(B ∣ Ai)×P(Ai)P(A_k\ |\ B) = \frac{P(A_k\cap B)}{P(B)} = \frac{P(B\ |\ A_k) \times P(A_k)}{\sum_i P(B\ |\ A_i) \times P(A_i)}

  • 先验概率 prior probability P(Ai)P(A_i): 在知道 B 发生与否之前的 AiA_i 发生的概率
  • 后证概率 posterior probability P(Ai∣B)P(A_i | B): 在知道 B 发生与否之后的 AiA_i 发生的概率
    贝叶斯定理作用是在得知信息 B 之后更新了先验概率

条件空间解决三门问题

我们可以将未知直接选的逻辑表达式写作 P(choose directly)=1/3P(\text{choose directly}) = 1 / 3
如果我们选择之后又知道某个门是羊，那么更换选中车的概率表达式 P(change∣know one sheep)P(\text{change} | \text{know one sheep})
定义事件 A:= 选中车, B:= 打开羊门
则有 P(B∣A)=1=P(B∣Ac)P(B|A) = 1 = P(B | A^c) 因为不管选什么主持人必定会打开一个门后有羊的门
我们需要知道 P(A∣B)P(A| B) 因此我们需要用贝叶斯公式 P(A∣B)=P(B∣A)×P(A)P(B)P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}
P(B)=P(B∣A)∗P(A)+P(B∣Ac)∗P(Ac)=1/3∗1+2/3∗1=1P(B) = P(B|A) * P(A) + P(B|A^c) * P(A^c) = 1/3 * 1 + 2/3 * 1 = 1
P(A∣B)=1/3∗1/1=1/3P(A|B) = 1/3 * 1 / 1 = 1/3
而选不中的概率是 P(Ac∣B)=1−P(A∣B)=2/3P(A ^c | B) = 1 - P(A|B) = 2/3