在使用抽象数据类型的时候，我们往往会需要考虑数据结构的存取api的使用逻辑，这我就需要考虑栈和队列了
数据的存储有两种形式: 连续的 array 型存储 和 离散的 linked list 型存储，我们接下来也会对比二者的效果

栈 Stack

栈的存储顺序是 LIFO, 即 last in - first out
需要两个指针: 指向栈底的 base_ptr 与 指向栈顶的 top_ptr , 其中 top_ptr 指向的是栈顶的下一个位置(悬空)

Method Implementation Array Complexity List Complexity
push 1. 可能需要申请二倍空间
2. 或者单纯将数据复制到 top 指针并且向后移动一位 top		 O(n)
O(1)		 O(1)
O(1)
pop 向前移动 top 指针 O(1) O(1)
top 返回 top 前一个指针并且去引用 O(1) O(1)
size 用 top 地址减去 base 地址 O(1) O(1)
empty 返回 base_ptr == top_ptr O(1) O(1)

注意申请空间的时间复杂度是 O(1), 而将数据从老的数组移动到新的数组中的时间复杂度是 O(n), 同时还有 delete 旧的数组, 时间复杂度也是 O(1). 总的时间复杂度 O(n)
虽然从复杂度分析上我们可以看出 array > list 但是实际应用中 array 用的更多，因为linked list的所需要的配置内存过大
不过，在应用中，deque 的使用更为广泛

队列 Queue

队列是一种 FIFO 的结构，first in first out
需要两个指针，一个指向队列的开头 front_idx, 另一个指向队列的结尾 end_idx
不过我们想知道，对于一个数组而言，如何利用好固定的内存并且让 base_ptr 能一直向后移动。
使用库为 #include <queue>, 不过常用的是 deque

循环队列 Circular Queue

将一个线性的数组等效为 一个环形的数组，即在填充完数组最后的位置后重新到数组的最开始的位置填充新的数据。
填充公式:

idx=(idx+1) % capacity\text{idx} = (\text{idx} + 1)\ \%\ \text{capacity}

不过如果循环队列的数据填满了，我们也需要申请更多的空间

pop 流程

直接将 front_idx 向后移动一个位置

空间申请流程

我们首先将现有的数据按照顺序排列成正序（要求 front_idx 放到第一个位置）
然后用 front_idx realloc 一个新的大存储空间

双向队列 Double-Ended Queue

功能: 能够高效的插入和移除 队列前面和后面的单元
注意 vector 本身并不具有 deque 的 push_front() 和 pop_front() 的两个方法
同样的 双向队列可以用 iterator 进行迭代访问，也可以使用 [] 直接访问元素内容，时间复杂度 O(1) , 因为这里利用的是指针地址进行偏移量推算，具体方法如下:

双向队列的内存形式

双向队列在内存中，按照 块 结构进行保存，首先多个小的连续的队列块放到一起，不同的块散列在内存的不同位置，因此我们找到双向队列某个元素的时候就需要计算 chunk 坐标和 offset/shift 偏移量
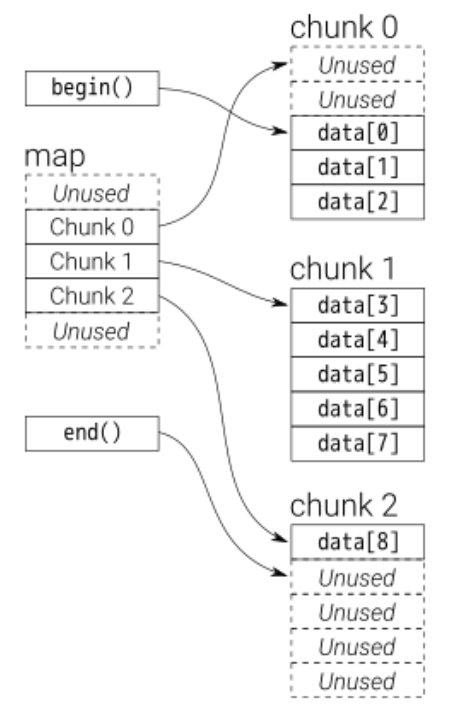
deque_chunk.png
因此这个过程的复杂度是 O(1) 而不是线性查找的 O(n)

优先队列 Priority Queue (PQ)

建议观看这个视频理解 bilibili
不同于一般队列的按照进入顺序排序，优先队列满足 优先级高的先出
c++库为 priority_queue

应用场景

  • 数据压缩：赫夫曼编码算法；
  • 最短路径算法：Dijkstra 算法；
  • 最小生成树算法：Prim 算法；
  • 任务调度器：根据优先级执行系统任务；
  • 排序问题：查找第 k 个最小元素。

传统实现方式局限性

假设我们用数字来代表任务存储在一个数组中，数字越大优先级越高。那么在排队的过程中数字是自动插到数组的结尾，因此时间复杂度 O(1)O(1)
但是在取出的过程中，我们需要先线性查找到最大数的位置 O(n)O(n)，将数组重新排序，时间复杂度 O(n)O(n)
但是我们看得出来这种排序方式效率非常低，所以我们可以考虑使用一个有序数组来存储这个优先队列
但是由于插入的时候要涉及冒泡排序，因此插入的时间复杂度为 O(n)O(n)
并且我们也经常用到数组空间的申请和销毁，这个时间复杂度也是 O(n)O(n)
因此我们可以联想到 用 链表 来完成这个艰巨的任务 来防止申请空间的线性复杂度，但是和 array 型存储一样，链表也会具有插入或者删除的线性复杂度（二者至少有其一）
如果在应用过程中明显有插入和删除的次数差异我们可以考虑使用上面的方法
不过，正如我们提到的，这种数据结构具有 不平衡 的特性，我们需要找一种办法将时间成本均摊到增删两步中，就能有效降低复杂度

二叉堆 Binary Heap

建堆操作

提取数组的第一个元素作为 “根” 元素，然后每来一个元素就与根比较大小，如果新元素大于根就与根进行换位操作，术语 “上浮”
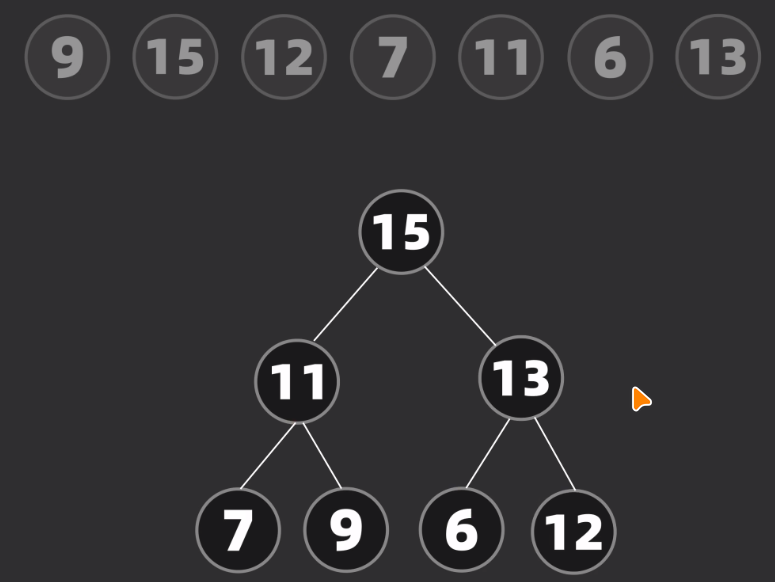
binary_heap_model.png
这里由于是从大到小进行堆放的，所以我们也叫它最大堆；如果是从小到大进行堆放，我们也叫它最小堆

索引

虽然结构上是满足堆的形式了，实际上仍然按照数组的形式进行存储，所以我们要定义一套索引系统方便我们根据坐标快速找到对应的元素
我们考察一份 根-左-右 模型，我们会发现三个节点的索引关系满足如下
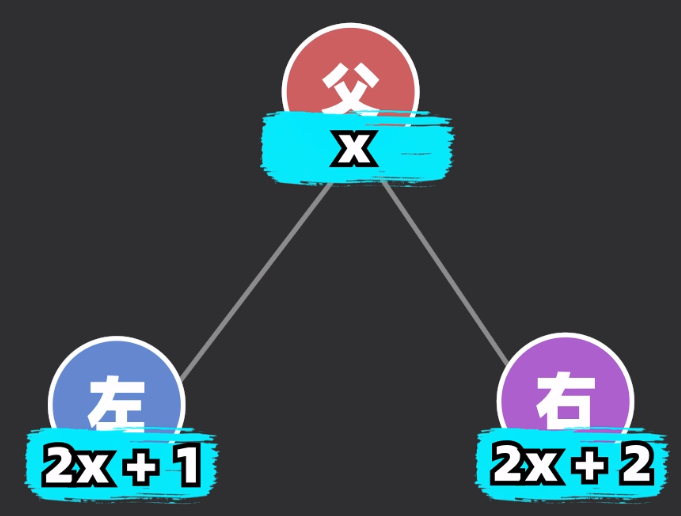
idx_heap.png
有了这个公式关系，我们就可以快速存储一个堆

优先队列实现

在最大堆中，最大元素（优先级最高元素）一般都会在堆的顶端，那么我们pop的对象就是堆顶元素，之后，我们再将堆顶元素进行 下沉 操作（就是和上浮相反的操作），如果顶同时小于左右两个元素，就和较大的换位置，这个时间复杂度由于满足二叉关系，只有 O(log⁡n)O(\log n)