你重生了，这一世，你是云汉交龙电控部的成员，部长要求你现在完成哨兵机器人的pitch轴云台调试，否则你会受到那个男人的锐评。那么我们从头从原理上开始理解一下 pid 的数学工程原理吧。

从闭环控制到 控制器

首先我们明确，pid控制是基于闭环控制的，也就是说，我们会用输出结果作为反馈和输入值进行比较，大了就减小，小了就增大，最后收敛到目标值
那么我们令输入参考值为 rr 输出值为 yy 我们经过二者的对比得到 r−y=er - y = e 定义为 error 误差，同时，我们 在控制对象的时候要将这个过程分成被控对象和控制器两部分 (名词命名、定义详见江苏教育出版社高中通用技术教科书，浙江省2022年技术高考教材)，比如对于一个空调房的温度控制，被控对象是房间，其自身的温度响应符合我们以前学过的热力学系统，即其温度对输入热量可以表述为一个传递函数，我们称之为 plant 写作 PP. 类似的，空调房的空调本调就是一个控制器 (controller) ，其控制的过程就是一个传递函数 CC 我们分开两部分进行描述就可以将被动系统和主动控制器进行拆分，从而更加明确控制参数对于效果的影响了
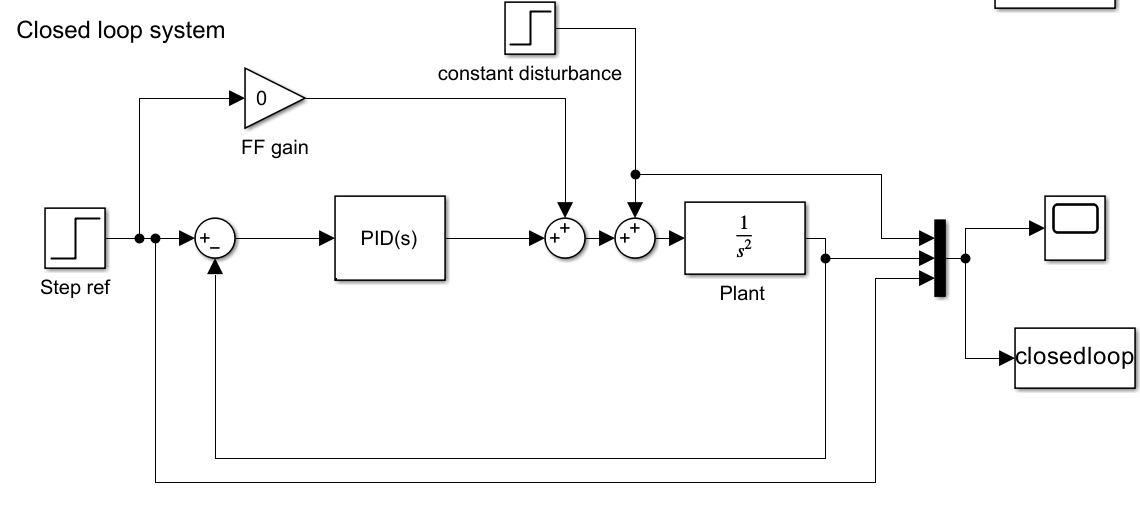
block_diagram
同样的，对于云台 pitch 控制, 我们有 pitch 轴为被控对象，pitch 电机 (6020) 为控制器, 云台自身重力是一个稳定偏差，我们对云台向下掰一掰就是一个 扰动输入，那么，从那个男人的视角，你要做到的，就是尽快回到原来的位置。
从下面开始，我们将讨论单位负反馈调节的系统 (unity negative feedforward system) 的pid 控制理论

P, I, D 是什么

首先明确，PID 本身是控制器 C 的固有参数，即 C=Kp+KDs+KIsC = K_p + K_Ds + \frac{K_I}{s} 这里是处在复频域的传递函数

Nomenclature

  • KpK_p Proportional Gain
  • KIK_I Integral Gain
  • KDK_D Derivative Gain
    对于解决偏差，我们最直接的想法就是用一个比例乘以error就能实现在error大的时候快速回正，errorr小的时候缓慢回正(这里是防止加速度过大超调) 所以我们令函数 C=KpeC = K_p e, 写成完整的传递函数，我们就有 H=CP1+CPH = \frac{CP}{1 + CP} 如果传递函数 P=11+sP = \frac{1}{1 + s} 那么我们有 H=Kps+(1+Kp)H = \frac{K_p}{s + (1 + K_p)} 这就是一个简单的比例控制器
    对于 step input 其终值为 Kp1+Kp\frac{K_p}{1 + K_p} 并不是 1, 也就是说，输出相对于输入并没有完全一样，会存在一个稳态误差 steady state error

工程拟合参数

作为不擅长数学的工程师，我们会用到以下这些近似公式简化对于预期结果的运算:

跃升时间 rise time trt_r

我们定义跃升时间为系统从 10% 到 90% 的时间，即 tr=t90−t10t_r = t_{90} - t_{10}

tr=1.8ωnt_r = \frac{1.8}{\omega_n}

稳定时间 settling time tst_s

稳定时间是指系统到达 98%98\% 或者 99%99\% 的时间

ts=4ζωn  (对应98)t_s = \frac{4}{\zeta \omega_n}\ \ (对应98)

ts=4.6ζωn  (对应99)t_s = \frac{4.6}{\zeta \omega_n}\ \ (对应99)

过阻尼系统的settling time

对于一个过阻尼系统，我们的解是实数，也就是说没有振动的频率分量. 解形式为 es1t+es2te^{s_1t} + e^{s_2t} 那么一般找大的那个(负数的绝对值小的)进行化简

ts=4min⁡∣s1∣,∣s2∣t_s = \frac{4}{\min{|s_1|,|s_2|}}

或者更简单的形式，我们用二次方程的解来描述
对于 s2+Ks+ωn2s^2 + Ks + \omega_n^2 的形式，我们有

−K+K2−1002<−4\frac{-K + \sqrt{K^2 - 100}}{2} < -4

超调比 Overshoot MpM_p

二阶系统超过水平稳定状态的比例

Mp=e−πζ/1−ζ2M_p = e^{-\pi \zeta / \sqrt{1 - \zeta^2}}

注意这里的公式的适用对象是 二阶系统对于 unit step input

前馈 Feedforward

对于一个稳定的误差（比如说重力）输入，我们如果忽略之，那么我们的稳态输出会存在一个误差，那么我们需要找到一个稳定的方式进行解决这个误差
首先，我们需要考虑将输入扩大几倍（倍数和稳态的缩减比例倒数确定）这种方法叫 pre-multiplication method 但是这种方法对于不同的 稳定误差的结果是不同的，很难确认，同时其往往需要放大输入，会造成能量的损失，工程上应用不是那么多
我们往往采用另一种方法：前馈 (Feedforward) 在这种方法中，我们将输入 reference 通过一个 feedforward gain （往往写作 L) 来将输入扩大一定倍数 添加到系统的 控制器后、plant 前
对于常见系统的前馈，我们可以将传递函数写成

H=CP+LP1+CPH = \frac{CP + LP}{1 + CP}