动力学分析: 速度, 加速度, 角加速度

平面运动 plane motion

位移

rB=rA+rB/Ar_B = r_A + r_{B/A}

速度 velocity

对于在一个刚体上的点 A, B, 我们有:

vB=vA+ω×rB/Av_B = v_A + \omega \times r_{B/A}

正弦定理 sin law

对于常见的 crank-slider, 即四连杆且有一个一维运动滑块, 我们连接 pin 和滑块得到一个三角形，对于这个三角形我们可以做正弦定理进行分析，详见 slides L9: 19

余弦定理 cos law

对于 crank-rocker 即非滑块四连杆，我们有一个四边形，通过连接对角线我们有两个三角形，对各自进行余弦定理运算可以获得对角线长度表达式，那么又变回了三角形形状分析即正弦定理分析

瞬心 instaneous center

对于刚体其所有点运动速度的垂线交点就是瞬心，对于平面运动，我们可以通过两个点的速度方向和大小来确定瞬心位置。瞬心的运动速度为 0 因此整个刚体相对于瞬心的运动可以看作是 pure rotation
利用和瞬心的几何关系，我们就可以获得速度大小之间的关系

加速度关系 acceleration

平面运动的刚体的加速度关系为 aA=aB+α×rB/A−ω2rB/Aa_A =a_B + \alpha \times r_{B/A} - \omega^2 r_{B/A}

旋转轴系的加速度推算

假设滑块在旋转轴系 xyz 的 x 轴上运动，但是 xyz 本身围绕 z 轴以 Ω\Omega 的角速度旋转，那么在固定坐标系 XYZ 下的加速度推算关系为

aB=aA+Ω˙×rB/A+Ω×(Ω×rB/A)+2Ω×(vB/A)xyz+(aB/A)xyza_B = a_A + \dot\Omega\times r_{B/A} + \Omega\times(\Omega\times r_{B/A}) + 2\Omega\times(v_{B/A})_{xyz} + (a_{B/A})_{xyz}

受力分析 Force Analysis

二力杆 two - force member

对于平衡态的杆，受到的两个力一定等大反向，同时作用于同一根线上，不然受力一定不平衡

三力杆 three - force member

用高中的话说，三力的矢量和为 0, 或者说当我们将受力分成 x 方向和 y 方向两个分量各自为 0
对于 crank-slider 结构，与 slider 相连的杆的受力方向一定沿着杆向，那么在 slider 处我们可以用三点受力平衡解算沿杆力大小
对于 与pin相连的杆子，我们则可以计算前面那根杆对于pin施加的力矩大小，再用力矩平衡解算沿驱动杆力矩大小
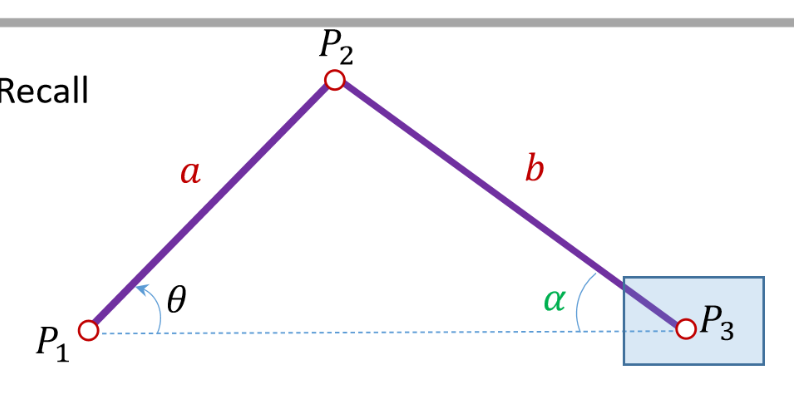
crank-slider

荡秋千模型

这是一种动态平行四边形结构，我们将秋千看作一个质点，那么这个秋千就是在做 变速圆周运动，我们沿著轨迹圆的切向和法相分别解算得到加速度，同时我们默认两根秋千索的力大小方向相同，即表现为 重力分量和离心力的平衡
同时我们有秋千角速度始终为零 (平行四边形对边平行，秋千平行于天花板)即关于其质心的扭矩和为 0
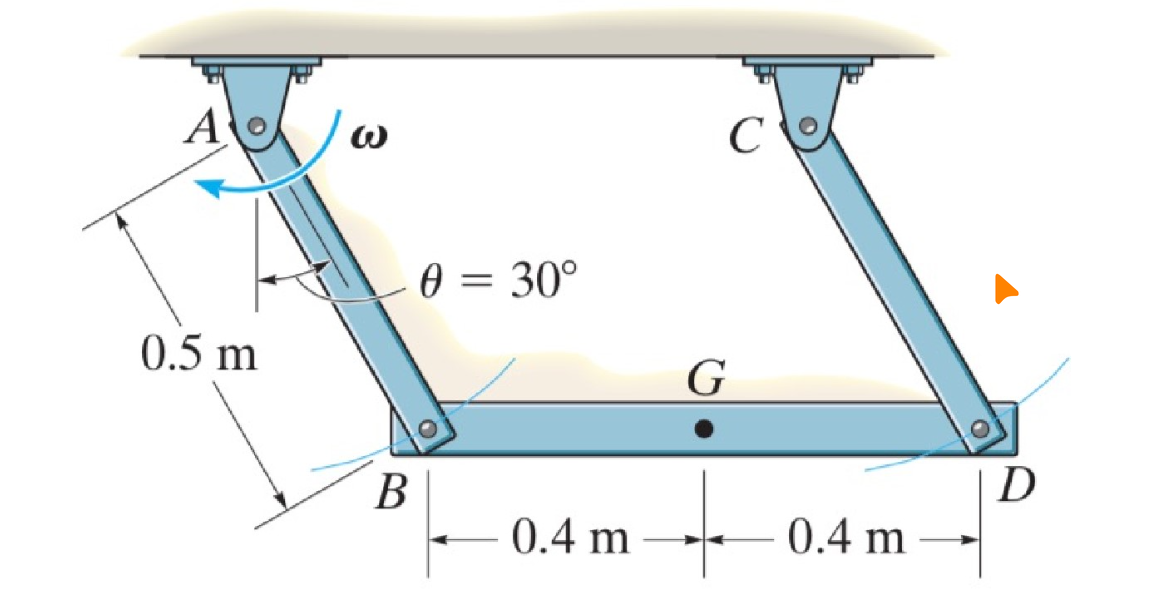
qiuqian

空间性机械结构 Spatial Mechanism

对于大部分的机械结构，我们都是用平面运动进行设计，但是也会存在不少的 3D 运动轨迹的机械结构

公式

M=6(L−1)−5j1−4j2−3j3−2j4−j5M = 6 (L-1) - 5j_1 - 4j_2 - 3j_3 - 2j_4 - j_5

其中 MM 表示 自由度

凸轮设计 Cam Design

分类 Classification

对于一个凸轮 - 从动轮的设计，我们可以根据从动轮接触面的形状，将此分类成 knife (尖端), flat face (平面), roller (滚轮)
以及通过从动轮的运动轨迹分为 平动 (translating) 和 旋转 (pivoting)

术语 Nomenclature

  • cam profile: 凸轮的表面形状
  • trace point: 对于 knife 形状的 follower 的尖端运动轨迹，或者对于 roller 的中心运动轨迹
  • pitch curve: 对于cam 而言的trace 轨迹
  • base circle: 凸轮的最小半径形成的圆，圆心就是凸轮的轴
  • prime circle: 和 pitch curve 最小相切圆
  • pressure angle: 凸轮法向和轨迹点运动方向成角
    • 对于平动轨迹而言，就是法向和平动方向成角
    • 工业上一半要越小越好，实际上不大于30°

位移图 Displacement Diagram

定义

一个凸轮转一圈的从动轮位移关于转动角度 θ\theta 的变化图像

专业名词

  • Rise: 从动轮上升（远离驱动轮圆心） （创造营2019男团x)
  • Dwell: 从动轮相对圆心静止
  • Fall / Return: 从动轮向圆心移动

运动的分类

对于 rise 或者 return，我们可以细分到每一部分的小运动形式，并且这些运动形式都可以遵循某些曲线形式

标准运动 uniform motion

符合线性关系

  • rise: s∗=Lθ∗βs^* = L\frac{\theta^*}{\beta}
  • return: s∗=L(1−θ∗β)s^* = L(1 - \frac{\theta^*}{\beta})
    • 注意这里 ∗* 表示局部运动，以下就省略了
    • β\beta 表示局部终点，如果假设局部起点为0
抛物线运动 parabolic motion

在动力学上可以解释为 常加速度运动

  • rise1(这下真创造营2019了): s=2L(θβ)2, (0≤θ≤β2)s = 2L(\frac{\theta}{\beta})^2,\ (0\le \theta\le \frac{\beta}{2})
  • rise2: L[−1+4θβ−2(θβ)2]L\left[ -1 + 4\frac{\theta}{\beta} - 2\left(\frac{\theta}{\beta}\right)^2\right]
  • return1: L[1−2(θβ)2]L\left[1 - 2\left(\frac{\theta}{\beta}\right)^2\right]
  • return2: LL
简谐运动 harmonic motion
  • rise: s=L2(1−cos⁡πθβ)s = \frac{L}{2}(1 - \cos\frac{\pi\theta}{\beta})
  • return: s=L2(1+cos⁡πθβ)s = \frac{L}{2}(1 + \cos\frac{\pi\theta}{\beta})
摆线运动 cycloidal motion
  • rise: s=L(θβ−12πsin⁡2πθβ)s = L(\frac{\theta}{\beta} - \frac{1}{2\pi}\sin\frac{2\pi\theta}{\beta})
  • return: s=L(1−θβ+12πsin⁡2πθβ)s = L(1 - \frac{\theta}{\beta} + \frac{1}{2\pi}\sin\frac{2\pi\theta}{\beta})

手绘凸轮外围的方法

  1. 画出凸轮的基圆
  2. 画出displacement diagram 位移曲线，其 x 轴与基圆的上界相切
  3. 选择位移曲线的 90, 180, 270 三个点对齐从圆心出来的竖线得到的交点
  4. 从基圆圆心到这些点作圆到其对应角度，再用平滑的曲线连接这些点
    1. 这里要注意区分，我们画的线是follower的运动曲线，如果 follower不是 knife 类型 那么我们要首先画出 follower 形状再得到 cam 的 profile
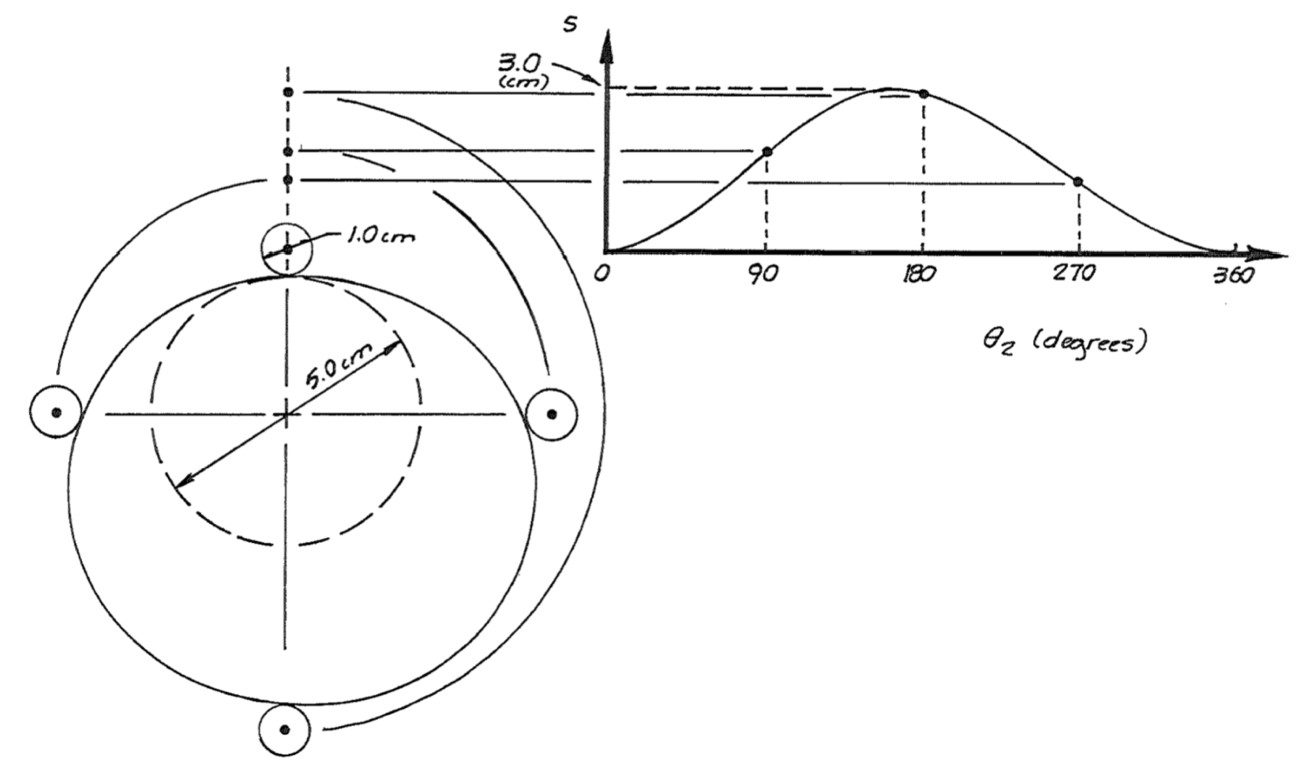
      cam_follower.png

齿轮组设计 Gear Design

减速比 speed ratio

齿轮 2 对 齿轮 1 的转速的比值，写作 e2/1=ω2ω1=N1N2e_{2/1} = \frac{\omega_2}{\omega_1} = \frac{N_1}{N_2}
更普遍的用法，就是输入齿数 / 输出齿数
同时注意正负号的使用，简单理解就是正正齿轮啮合为负号，正负齿轮啮合为正
那怎么判断正负齿轮呢？正齿轮就是两个轴在交线的两侧，正负齿轮两个轴在交线的同一侧
或者，我们可以用相交点的转动方向相同来具体推算某个齿轮的转动方向

Nomenclature

  • pc=πdN [in]p_c = \frac{\pi d}{N}\ [in], circular pitch
  • P=NdP = \frac{N}{d}, diametral pitch
    • pcP=πp_c P = \pi
  • m=dNm = \frac{d}{N}, module

内外圆

addendum 额外圆 a

齿轮外圆半径(或者直径)减去齿轮基圆半径 (或者直径)

dedendum 减量圆 b

齿轮基圆半径减去齿轮内圆半径

clearance 公差 b - a

行星齿轮组 Planetary Gear Trains

Nomenclature

  • sun gear: 中心齿轮
  • ring gear: 外环齿轮
  • crank (planet carrier): 行星轴

制表法求解行星齿轮组转速

  1. 假设行星齿轮组的所有元素按照 xx 角速度进行旋转 (这里说的是绝对角速度，因此实际上两个齿轮之间是没有相对转速的)
  2. 第二种情况假设crank 固定，驱动轮按照 yy 进行旋转这样就变成了固定齿轮组转速的估计
  3. 由于前面两种情况线性独立，那么我们将两个变量相加就能得到最终的转速

差速器 Differentials

对于一个汽车的轴，我们希望能通过一个输入转速就能驱动两个轮子以同样的速度向前，但是也可以存在一个较小的速度差（比如我们在排水渠过弯的时候由于左右轮子的运动半径不同所以转速不同）
转速关系:

ωtot=ωleft+ωright2\omega_{tot} = \frac{\omega_{left} + \omega_{right}}{2}